2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
23. (本小题满分11分)
新情境 古代智慧 根据素材,完成探究任务:城墙建多高才能抵御进攻方的进攻.
【素材呈现】
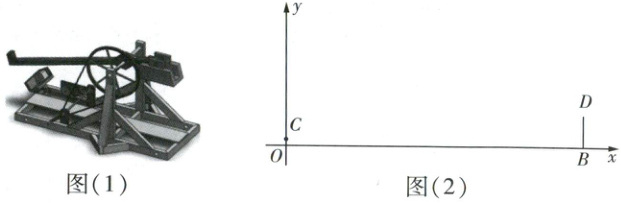
如图(1)是古代进攻方的一种攻城器械“发石车”.如图(2),防守方城墙BD=10 m,垂直于地面OB,进攻方把“发石车”放置在距B处90 m的O处,石块从O处竖直方向上的C处被投出,当石块在空中飞行到与OC的水平距离为50 m时,石块离地面OB的高度最高,为27 m.
【解决问题】
(1) 当OC=2 m时,
①参照图(2)所建立的坐标系,求抛物线(石块运动轨迹)的解析式.
②进攻方的石块能飞进防守方的城墙吗?若能,城墙应加建多高以上,才能让进攻方的石块飞不进防守方城墙;若不能,请说明理由.
(2) 石块出发点C与O的距离在什么范围内,防守方无须加高城墙?
新情境 古代智慧 根据素材,完成探究任务:城墙建多高才能抵御进攻方的进攻.
【素材呈现】
如图(1)是古代进攻方的一种攻城器械“发石车”.如图(2),防守方城墙BD=10 m,垂直于地面OB,进攻方把“发石车”放置在距B处90 m的O处,石块从O处竖直方向上的C处被投出,当石块在空中飞行到与OC的水平距离为50 m时,石块离地面OB的高度最高,为27 m.
【解决问题】
(1) 当OC=2 m时,
①参照图(2)所建立的坐标系,求抛物线(石块运动轨迹)的解析式.
②进攻方的石块能飞进防守方的城墙吗?若能,城墙应加建多高以上,才能让进攻方的石块飞不进防守方城墙;若不能,请说明理由.
(2) 石块出发点C与O的距离在什么范围内,防守方无须加高城墙?

答案:
23 名师教审题 函数的实际应用题系列
审题后,将获取的信息在图中标注出来,如下图。

解决第
(1)②问的关键:

(1)①
∵OC = 2m,
∴C(0, 2)。(1分)
设抛物线的解析式为y = a(x - 50)² + 27(点拨:知道顶点坐标,故设顶点式),
将C(0, 2)代入,得2 = a(0 - 50)² + 27,
解得a = - $\frac{1}{100}$,(3分)
∴抛物线的解析式为y = - $\frac{1}{100}$(x - 50)² + 27。(4分)
②进攻方的石块能飞进防守方的城墙。
∵BD = 10m,OB = 90m,
∴D(90, 10)。
当x = 90时,y = - $\frac{1}{100}$×(90 - 50)² + 27 = 11。(7分)
∵11 > 10,
∴进攻方的石块能飞进防守方的城墙。(8分)
11 - 10 = 1(m),
∴城墙应加高1m以上。(9分)
(2)设OC = nm,则C(0, n)。
设抛物线的解析式为y = b(x - 50)² + 27,
将C(0, n)代入,得n = b(0 - 50)² + 27,
∴b = $\frac{n - 27}{2500}$,
∴抛物线的解析式为y = $\frac{n - 27}{2500}$(x - 50)² + 27。
由$\frac{n - 27}{2500}$(90 - 50)² + 27 < 10,解得n < $\frac{7}{16}$,
∴当OC < $\frac{7}{16}$m时,防守方无须加高城墙。(11分)
23 名师教审题 函数的实际应用题系列
审题后,将获取的信息在图中标注出来,如下图。

解决第
(1)②问的关键:

(1)①
∵OC = 2m,
∴C(0, 2)。(1分)
设抛物线的解析式为y = a(x - 50)² + 27(点拨:知道顶点坐标,故设顶点式),
将C(0, 2)代入,得2 = a(0 - 50)² + 27,
解得a = - $\frac{1}{100}$,(3分)
∴抛物线的解析式为y = - $\frac{1}{100}$(x - 50)² + 27。(4分)
②进攻方的石块能飞进防守方的城墙。
∵BD = 10m,OB = 90m,
∴D(90, 10)。
当x = 90时,y = - $\frac{1}{100}$×(90 - 50)² + 27 = 11。(7分)
∵11 > 10,
∴进攻方的石块能飞进防守方的城墙。(8分)
11 - 10 = 1(m),
∴城墙应加高1m以上。(9分)
(2)设OC = nm,则C(0, n)。
设抛物线的解析式为y = b(x - 50)² + 27,
将C(0, n)代入,得n = b(0 - 50)² + 27,
∴b = $\frac{n - 27}{2500}$,
∴抛物线的解析式为y = $\frac{n - 27}{2500}$(x - 50)² + 27。
由$\frac{n - 27}{2500}$(90 - 50)² + 27 < 10,解得n < $\frac{7}{16}$,
∴当OC < $\frac{7}{16}$m时,防守方无须加高城墙。(11分)
24. (本小题满分12分)
如图(1),在△ABC中,AB=AC,∠BAC=90°,BC=16.过点A作AD⊥BC于点D,E为腰AC上一动点,连接DE,以DE为斜边向左上方作等腰直角三角形DEF.
(1) 当点F落在线段AD上时,如图(2),求证:AF=EF.
(2) 在点E的运动过程中,若$S_{△DEF}=9$,求线段CE的长.
(3) 在点E从点C运动到点A的过程中,
①直接写出点F运动的路径长;
②连接AF,若AF=5,直接写出线段AE的长.
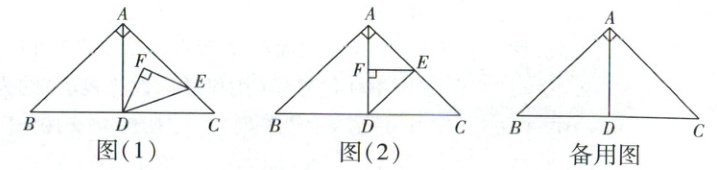
如图(1),在△ABC中,AB=AC,∠BAC=90°,BC=16.过点A作AD⊥BC于点D,E为腰AC上一动点,连接DE,以DE为斜边向左上方作等腰直角三角形DEF.
(1) 当点F落在线段AD上时,如图(2),求证:AF=EF.
(2) 在点E的运动过程中,若$S_{△DEF}=9$,求线段CE的长.
(3) 在点E从点C运动到点A的过程中,
①直接写出点F运动的路径长;
②连接AF,若AF=5,直接写出线段AE的长.

答案:
24
(1)证明:
∵AB = AC = 16,∠BAC = 90°,AD⊥BC,
∴∠CAD = 45°。(1分)
∵△EFD是等腰直角三角形,
∴∠EFD = ∠AFE = 90°,
∴∠AEF = 180° - ∠CAD - ∠AFE = 45°,
∴∠EAF = ∠AEF,(3分)
∴AF = EF。(4分)
(2)如图
(1),取AC的中点M,连接DM。
由题意知△ACD是等腰直角三角形,
∴DM⊥AC。
∵AB = AC,AD⊥BC,BC = 16,
∴CD = 8,
∴CM = DM = $\frac{\sqrt{2}}{2}$CD = 4$\sqrt{2}$。(5分)

∵S_{△EFD} = $\frac{1}{2}$EF·DF = $\frac{1}{2}$EF² = 9,
∴EF = 3$\sqrt{2}$,
∴DE = $\sqrt{2}$EF = 6,(7分)
∴EM = $\sqrt{DE^{2}-DM^{2}}$ = 2,(8分)
∴CE = 4$\sqrt{2}$ + 2或4$\sqrt{2}$ - 2。(9分)
一题多解

AB = AC,∠BAC = 90°,AD⊥BC,BC = 16
CD = 8,∠C = 45°
设CN = x,则EN = x,DN = DC - CN = 8 - x。
S_{△EFD} = $\frac{1}{2}$EF·DF = $\frac{1}{2}$EF² = 9
∴EF = 3$\sqrt{2}$,DE = $\sqrt{2}$EF = 6。
在Rt△DEN中,根据勾股定理,得DE² = DN² + EN²,
即6² = (8 - x)² + x²(点拨:根据勾股定理列方程),
解得x₁ = 4 + $\sqrt{2}$,x₂ = 4 - $\sqrt{2}$,
∴CE = 4$\sqrt{2}$ + 2或4$\sqrt{2}$ - 2。
(3)①8。(10分)
解法提示:
如图
(2),取AC的中点M,连接DM,MF;
巧作辅助线:多次画图,猜想点F在△ABC的中位线上,故作DM,恰好出现“手拉手”模型

易证△DMC是等腰直角三角形。
∵△DEF是等腰直角三角形,
∴$\frac{DM}{DC}$ = $\frac{DF}{DE}$ = $\frac{\sqrt{2}}{2}$,∠FDE = ∠MDC = 45°,
∴∠FDM = ∠EDC,
∴△FDM∽△EDC(点拨:“手拉手”模型),
∴∠FMD = ∠C = 45° = ∠MDC,
∴FM//BC。
延长MF交AB于点G,则MG是△ABC的中位线。
分析可知,当点E从点C运动到点A时,点F从点M沿MG运动到点G,
∴点F运动的路径长为8。
②7$\sqrt{2}$或$\sqrt{2}$。(12分)
解法提示:当AF = 5时,如图
(3)或图
(4)所示,设直线MF与AD交于点P,易知MP⊥AD,AP = MP = $\frac{1}{2}$CD = 4,


∴PF = $\sqrt{AF^{2}-AP^{2}}$ = 3。
由①知△FDM∽△EDC,
∴$\frac{FM}{EC}$ = $\frac{DM}{DC}$ = $\frac{\sqrt{2}}{2}$,
∴EC = $\sqrt{2}$FM。
易得AC = $\frac{\sqrt{2}}{2}$BC = 8$\sqrt{2}$。
a. 当点F在AD右侧时,如图
(3),FM = PM - PF = 1,
∴EC = $\sqrt{2}$,
∴AE = AC - CE = 7$\sqrt{2}$。
b. 当点F在AD左侧时,如图
(4),FM = PM + PF = 7,
∴EC = 7$\sqrt{2}$,
∴AE = AC - EC = $\sqrt{2}$。
综上所述,线段AE的长为7$\sqrt{2}$或$\sqrt{2}$。
24
(1)证明:
∵AB = AC = 16,∠BAC = 90°,AD⊥BC,
∴∠CAD = 45°。(1分)
∵△EFD是等腰直角三角形,
∴∠EFD = ∠AFE = 90°,
∴∠AEF = 180° - ∠CAD - ∠AFE = 45°,
∴∠EAF = ∠AEF,(3分)
∴AF = EF。(4分)
(2)如图
(1),取AC的中点M,连接DM。
由题意知△ACD是等腰直角三角形,
∴DM⊥AC。
∵AB = AC,AD⊥BC,BC = 16,
∴CD = 8,
∴CM = DM = $\frac{\sqrt{2}}{2}$CD = 4$\sqrt{2}$。(5分)

∵S_{△EFD} = $\frac{1}{2}$EF·DF = $\frac{1}{2}$EF² = 9,
∴EF = 3$\sqrt{2}$,
∴DE = $\sqrt{2}$EF = 6,(7分)
∴EM = $\sqrt{DE^{2}-DM^{2}}$ = 2,(8分)
∴CE = 4$\sqrt{2}$ + 2或4$\sqrt{2}$ - 2。(9分)
一题多解

AB = AC,∠BAC = 90°,AD⊥BC,BC = 16
CD = 8,∠C = 45°
设CN = x,则EN = x,DN = DC - CN = 8 - x。
S_{△EFD} = $\frac{1}{2}$EF·DF = $\frac{1}{2}$EF² = 9
∴EF = 3$\sqrt{2}$,DE = $\sqrt{2}$EF = 6。
在Rt△DEN中,根据勾股定理,得DE² = DN² + EN²,
即6² = (8 - x)² + x²(点拨:根据勾股定理列方程),
解得x₁ = 4 + $\sqrt{2}$,x₂ = 4 - $\sqrt{2}$,
∴CE = 4$\sqrt{2}$ + 2或4$\sqrt{2}$ - 2。
(3)①8。(10分)
解法提示:
如图
(2),取AC的中点M,连接DM,MF;
巧作辅助线:多次画图,猜想点F在△ABC的中位线上,故作DM,恰好出现“手拉手”模型

易证△DMC是等腰直角三角形。
∵△DEF是等腰直角三角形,
∴$\frac{DM}{DC}$ = $\frac{DF}{DE}$ = $\frac{\sqrt{2}}{2}$,∠FDE = ∠MDC = 45°,
∴∠FDM = ∠EDC,
∴△FDM∽△EDC(点拨:“手拉手”模型),
∴∠FMD = ∠C = 45° = ∠MDC,
∴FM//BC。
延长MF交AB于点G,则MG是△ABC的中位线。
分析可知,当点E从点C运动到点A时,点F从点M沿MG运动到点G,
∴点F运动的路径长为8。
②7$\sqrt{2}$或$\sqrt{2}$。(12分)
解法提示:当AF = 5时,如图
(3)或图
(4)所示,设直线MF与AD交于点P,易知MP⊥AD,AP = MP = $\frac{1}{2}$CD = 4,


∴PF = $\sqrt{AF^{2}-AP^{2}}$ = 3。
由①知△FDM∽△EDC,
∴$\frac{FM}{EC}$ = $\frac{DM}{DC}$ = $\frac{\sqrt{2}}{2}$,
∴EC = $\sqrt{2}$FM。
易得AC = $\frac{\sqrt{2}}{2}$BC = 8$\sqrt{2}$。
a. 当点F在AD右侧时,如图
(3),FM = PM - PF = 1,
∴EC = $\sqrt{2}$,
∴AE = AC - CE = 7$\sqrt{2}$。
b. 当点F在AD左侧时,如图
(4),FM = PM + PF = 7,
∴EC = 7$\sqrt{2}$,
∴AE = AC - EC = $\sqrt{2}$。
综上所述,线段AE的长为7$\sqrt{2}$或$\sqrt{2}$。
查看更多完整答案,请扫码查看


