《2026年金考卷中考45套汇编数学河北专版》

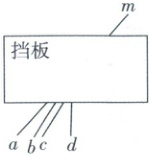
1. 如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一直线上,请借助直尺判断该线段是 (A)


A.a
B.b
C.c
D.d

答案：
1A 如图,利用直尺作线段$m$的延长线,可知线段$a$与线段$m$在同一直线上.

2. 不一定相等的一组是 (D)

A.$a + b$与$b + a$
B.$3a$与$a + a + a$
C.$a^{3}$与$a · a · a$
D.$3(a + b)$与$3a + b$

答案： 2D 根据加法交换律可知$a+b=b+a$;根据合并同类项法则可知$a+a+a=(1+1+1)a=3a$;根据乘方的意义可知$a· a· a=a^{3}$;根据乘法分配律可知$3(a+b)=3a+3b$,$3a+3b$与$3a+b$不一定相等.故选D.

3. 已知$a ＞ b$,则一定有$-4a□ -4b$,“$□$”中应填的符号是 (B)

A.$＞$
B.$＜$
C.$\geqslant$
D.$=$

答案： 3B 根据不等式的性质3(提示:不等式的两边都乘(或除以)同一个负数,不等号的方向改变),可知$-4a＜-4b$.

4. 与$\sqrt{3^{2} - 2^{2} - 1^{2}}$结果相同的是 (A)

A.$3 - 2 + 1$
B.$3 + 2 - 1$
C.$3 + 2 + 1$
D.$3 - 2 - 1$

答案： 4A $\sqrt{3^{2}-2^{2}-1^{2}}=\sqrt{9-4-1}=\sqrt{4}=2$，$3 - 2 + 1 = 2$，$3 + 2 - 1 = 4$，$3 + 2 + 1 = 6$，$3 - 2 - 1 = 0$，故选A.

5. 能与$-(\frac{3}{4} - \frac{6}{5})$相加得0的是 (C)

A.$-\frac{3}{4} - \frac{6}{5}$
B.$\frac{6}{5} + \frac{3}{4}$
C.$-\frac{6}{5} + \frac{3}{4}$
D.$-\frac{3}{4} + \frac{6}{5}$

答案： 5C $-(\frac{3}{4}-\frac{6}{5})$的相反数是$\frac{3}{4}-\frac{6}{5}$，即$-(\frac{3}{4}-\frac{6}{5})$与$\frac{3}{4}-\frac{6}{5}$相加得0，故选C.

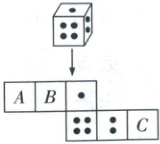
6. 一个骰子相对两面的点数之和为7,它的展开图如图,下列判断正确的是 (A)


A.A代表
B.B代表
C.C代表
D.B代表

答案：
6A 由展开图可知A与●相对，C与∙∙相对，B与∙相对.
∵相对两面的点数之和为7，
∴A代表∙∙，C代表∙，B代表∙∙，故选A.
名师敲重点 两要点归纳：
(1)“一四一”型:

(2)“一三二”型:

(3)“二二二”型:

(4)“三三”型:
(注:相同颜色表示相对的面)

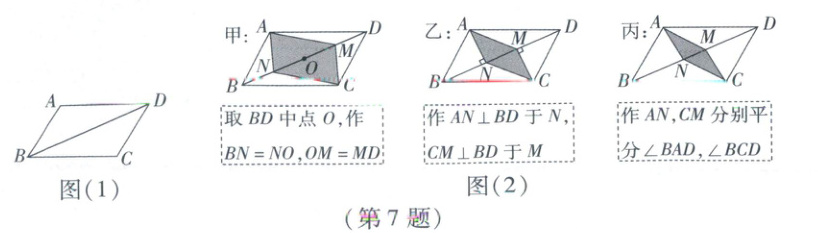
7. 如图(1),$□ ABCD$中,$AD ＞ AB$,$\angle ABC$为锐角,要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图(2)中的甲、乙、丙三种方案,则正确的方案 (A)


A.甲、乙、丙都是
B.只有甲、乙才是
C.只有甲、丙才是
D.只有乙、丙才是

答案： 7A 对于甲方案，连接AC，
∵四边形ABCD是平行四边形，
∴AC经过BD的中点O，且AO = CO.
∵BO = DO，BN = NO，
OM = MD，
∴NO = OM，
∴四边形ANCM是平行四边形(依据:对角线互相平分的四边形是平行四边形).对于乙方案，
易证△ABN≌△CDM，
∴AN = CM；
∵AN⊥BD，CM⊥BD，
∴AN//CM，
∴四边形ANCM是平行四边形(依据:一组对边平行且相等的四边形是平行四边形).对于丙方案，由平行四边形的性质及角平分线的性质可证△BAN≌△DCM，
∴AN = CM，∠ANB = ∠CMD，
∴∠ANM = ∠CMN，
∴AN//CM，
∴四边形ANCM是平行四边形(依据:一组对边平行且相等的四边形是平行四边形).综上可知，甲、乙、丙三种方案都是正确的.

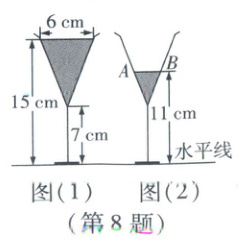
8. 图(1)是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图(2)所示,此时液面$AB$ = (C)


A.1 cm
B.2 cm
C.3 cm
D.4 cm

答案： 8C 根据“相似三角形对应高的比等于相似比”可知$\frac{6}{AB}=\frac{15 - 7}{11 - 7}$，即$\frac{6}{AB}=\frac{8}{4}$，
∴AB = 3cm.
名师碎碎念 如果两个三角形相似，那么它们对应边、对应中线、对应角平分线、对应高、周长的比都等于相似比，只有面积的比不等于相似比，而是等于相似比的平方，切勿混淆.