2026年学易优同步学案导学高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优同步学案导学高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第255页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
- 第216页
- 第217页
- 第218页
- 第219页
- 第220页
- 第221页
- 第222页
- 第223页
- 第224页
- 第225页
- 第226页
- 第227页
- 第228页
- 第229页
- 第230页
- 第231页
- 第232页
- 第233页
- 第234页
- 第235页
- 第236页
- 第237页
- 第238页
- 第239页
- 第240页
- 第241页
- 第242页
- 第243页
- 第244页
- 第245页
- 第246页
- 第247页
- 第248页
- 第249页
- 第250页
- 第251页
- 第252页
- 第253页
- 第254页
- 第255页
- 第256页
- 第257页
- 第258页
- 第259页
- 第260页
- 第261页
- 第262页
- 第263页
- 第264页
10. 若 $ \log _{\frac{1}{2}} x=m, \log _{\frac{1}{4}} y=m+2 $,求 $ \frac{x^{2}}{y} $ 的值.
答案:
10.解
∵log$\frac{1}{2}$x=m,
∴$(\frac{1}{2})^{m}=x$,$x^{2}=(\frac{1}{2})^{2m}$
∵log$\frac{1}{2}$y=m + 2,
∴$(\frac{1}{4})^{m + 2}=y$,$y=(\frac{1}{2})^{2m + 4}$
∴$\frac{x^{2}}{y}=\frac{(\frac{1}{2})^{2m}}{(\frac{1}{2})^{2m+4}}=(\frac{1}{2})^{2m-(2m+4)}=(\frac{1}{2})^{-4}=16$.
∵log$\frac{1}{2}$x=m,
∴$(\frac{1}{2})^{m}=x$,$x^{2}=(\frac{1}{2})^{2m}$
∵log$\frac{1}{2}$y=m + 2,
∴$(\frac{1}{4})^{m + 2}=y$,$y=(\frac{1}{2})^{2m + 4}$
∴$\frac{x^{2}}{y}=\frac{(\frac{1}{2})^{2m}}{(\frac{1}{2})^{2m+4}}=(\frac{1}{2})^{2m-(2m+4)}=(\frac{1}{2})^{-4}=16$.
11. (多选)下列命题正确的是(
A.若 $ \log$_${\sqrt{2}} x=3 $,则 $ x=2 \sqrt{2} $
$B.$若$ \log_{x} \frac{1}{16}=-\frac{2}{3} ,$则$ x=64 $
$C.$若$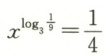
,$则$ x=4 $
$D.$若$ \log_{a^{2}} b^{2}=1 ,$则$ a=b $
AB
)A.若 $ \log$_${\sqrt{2}} x=3 $,则 $ x=2 \sqrt{2} $
$B.$若$ \log_{x} \frac{1}{16}=-\frac{2}{3} ,$则$ x=64 $
$C.$若$
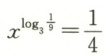
,$则$ x=4 $
$D.$若$ \log_{a^{2}} b^{2}=1 ,$则$ a=b $
答案:
11.AB 由log$\sqrt{2}$x=3,得$x=(\sqrt{2})^{3}=2\sqrt{2}$,则A正确;由logx$\frac{1}{16}$=$-\frac{2}{3}$,得$x^{-\frac{2}{3}}=\frac{1}{16}=2^{-4}$,则$(x^{-\frac{2}{3}})^{-\frac{3}{2}}=x$,所以$x=(2^{-4})^{-\frac{3}{2}}=2^{6}=64$,则B正确;
由3−2=$\frac{1}{9}$,得log3$\frac{1}{9}$=−2,所以$x^{-2}=\frac{1}{4}$,即$x = 2$或$x=-2$,则C不正确;
D中,a,b可能互为相反数.
由3−2=$\frac{1}{9}$,得log3$\frac{1}{9}$=−2,所以$x^{-2}=\frac{1}{4}$,即$x = 2$或$x=-2$,则C不正确;
D中,a,b可能互为相反数.
12. 将 $ a^{2 b}=N(a>0 $ 且 $ a \neq 1) $ 转化为对数形式,其中错误的是(
$A. b=\frac{1}{2} \log_{a} N $
$B. b=\log_{a^{2}} N $
$C. \log_{a^{b}} N=2 $
$D. b=\log_{a} \frac{N}{2} $
D
)$A. b=\frac{1}{2} \log_{a} N $
$B. b=\log_{a^{2}} N $
$C. \log_{a^{b}} N=2 $
$D. b=\log_{a} \frac{N}{2} $
答案:
12.D 若a2b=N,则2b=logaN,即$b=\frac{1}{2}\log_{a}N$,所以A正确;
若a2b=N,则(a²)b=N,即$b=\log_{a^{2}}N$,所以B正确;
若a2b=N,则(ab)²=N,即$2=\log_{a^{b}}N$,所以C正确;
由$b=\log_{\frac{N}{2}}a$得$a^{b}=\frac{N}{2}$,与已知a2b=N不相等,所以D错误.
若a2b=N,则(a²)b=N,即$b=\log_{a^{2}}N$,所以B正确;
若a2b=N,则(ab)²=N,即$2=\log_{a^{b}}N$,所以C正确;
由$b=\log_{\frac{N}{2}}a$得$a^{b}=\frac{N}{2}$,与已知a2b=N不相等,所以D错误.
13. 化简 等于(
等于(
A.14
B.0
C.1
D.6
 等于(
等于(B
)A.14
B.0
C.1
D.6
答案:
13.B 原式=4 -
(33)$^{\frac{2}{3}}$ - lg$\frac{1}{100}$ + 3 = 4 - 3² - ( - 2) + 3 = 0.
(33)$^{\frac{2}{3}}$ - lg$\frac{1}{100}$ + 3 = 4 - 3² - ( - 2) + 3 = 0.
14. 若 $ a=\lg 2, b=\lg 3 $,则 $ 100^{a-\frac{b}{2}} $ 的值为
$\frac{4}{3}$
.
答案:
14.$\frac{4}{3}$
∵a = lg2,
∴10a=2.
∵b = lg3,
∴10b=3.
∴100a - $\frac{b}{2}$=$\frac{(10^{2})^{a}}{(10^{a})^{\frac{b}{2}}}=\frac{(10^{a})^{2}}{10^{b}}=\frac{4}{3}$.
∵a = lg2,
∴10a=2.
∵b = lg3,
∴10b=3.
∴100a - $\frac{b}{2}$=$\frac{(10^{2})^{a}}{(10^{a})^{\frac{b}{2}}}=\frac{(10^{a})^{2}}{10^{b}}=\frac{4}{3}$.
15. 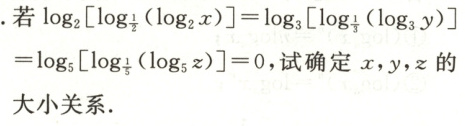
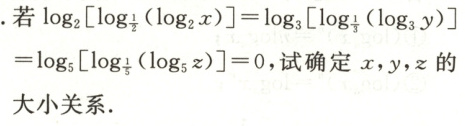
答案:
15.解 由log2[log$\frac{1}{2}$(log2x)] = 0,
得log$\frac{1}{2}$(log2x)=$\frac{1}{2}$,$\log_{2}x=2^{-\frac{1}{2}}=(2^{15})^{\frac{1}{30}}$,$x = 2^{\frac{1}{2}}=(2^{15})^{\frac{1}{30}}$.
由log3[log$\frac{1}{3}$(log3y)] = 0,
得log$\frac{1}{3}$(log3y)=1,$\log_{3}y=\frac{1}{3}$,$y = 3^{\frac{1}{3}}=(3^{10})^{\frac{1}{30}}$.
由log5[log$\frac{1}{5}$(log5z)] = 0,
得log$\frac{1}{5}$(log5z)=$\frac{1}{5}$,$\log_{5}z=\frac{1}{5}$,$z = 5^{\frac{1}{5}}=(5^{6})^{\frac{1}{30}}$,
∵310>215>56,
∴y>x>z.
得log$\frac{1}{2}$(log2x)=$\frac{1}{2}$,$\log_{2}x=2^{-\frac{1}{2}}=(2^{15})^{\frac{1}{30}}$,$x = 2^{\frac{1}{2}}=(2^{15})^{\frac{1}{30}}$.
由log3[log$\frac{1}{3}$(log3y)] = 0,
得log$\frac{1}{3}$(log3y)=1,$\log_{3}y=\frac{1}{3}$,$y = 3^{\frac{1}{3}}=(3^{10})^{\frac{1}{30}}$.
由log5[log$\frac{1}{5}$(log5z)] = 0,
得log$\frac{1}{5}$(log5z)=$\frac{1}{5}$,$\log_{5}z=\frac{1}{5}$,$z = 5^{\frac{1}{5}}=(5^{6})^{\frac{1}{30}}$,
∵310>215>56,
∴y>x>z.
查看更多完整答案,请扫码查看


