2026年学易优同步学案导学高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优同步学案导学高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第194页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
- 第216页
- 第217页
- 第218页
- 第219页
- 第220页
- 第221页
- 第222页
- 第223页
- 第224页
- 第225页
- 第226页
- 第227页
- 第228页
- 第229页
- 第230页
- 第231页
- 第232页
- 第233页
- 第234页
- 第235页
- 第236页
- 第237页
- 第238页
- 第239页
- 第240页
- 第241页
- 第242页
- 第243页
- 第244页
- 第245页
- 第246页
- 第247页
- 第248页
- 第249页
- 第250页
- 第251页
- 第252页
- 第253页
- 第254页
- 第255页
- 第256页
- 第257页
- 第258页
- 第259页
- 第260页
- 第261页
- 第262页
- 第263页
- 第264页
10. 已知集合 $ A = \{ x | - 3 \leq x \leq 4 \} $,$ B = \{ x | 2m - 1 < x < m + 1 \} $.
(1) 若 $ m = - 3 $,求 $ A \cap B $;
(2) 若 $ A \cup B = A $,求实数 $ m $ 的取值范围.
(1) 若 $ m = - 3 $,求 $ A \cap B $;
(2) 若 $ A \cup B = A $,求实数 $ m $ 的取值范围.
答案:
10.解
(1)当m=-3时,B={x∣-7<x<-2},
故A∩B={x∣-3≤x<-2}.
(2)因为A∪B=A,故B⊆A,
若2m−1≥m+1,即m≥2,则B=∅,符合题意;
若m<2,则{2m−1≥−3,m+1≤−2,
解得−1≤m<2,
综上,实数m的取值范围是{m∣m≥−1}.
(1)当m=-3时,B={x∣-7<x<-2},
故A∩B={x∣-3≤x<-2}.
(2)因为A∪B=A,故B⊆A,
若2m−1≥m+1,即m≥2,则B=∅,符合题意;
若m<2,则{2m−1≥−3,m+1≤−2,
解得−1≤m<2,
综上,实数m的取值范围是{m∣m≥−1}.
11. 已知集合 $ A = \{ x | - 2 < x < 4 \} $,集合 $ B = \{ x | x + a - 1 \geq 0 \} $,若 $ A \cup B = \{ x | x > - 2 \} $,则实数 $ a $ 的取值范围为(
A.$ - 2 < a < 3 $
B.$ - 3 \leq a < 3 $
C.$ - 3 \leq a < 4 $
D.$ a < 4 $
B
)A.$ - 2 < a < 3 $
B.$ - 3 \leq a < 3 $
C.$ - 3 \leq a < 4 $
D.$ a < 4 $
答案:
11.B 集合A={x∣-2<x<4},集合B={x∣x≥1−a},
若A∪B={x∣x>−2},则−2<1−a≤4,解得−3≤a<3.
若A∪B={x∣x>−2},则−2<1−a≤4,解得−3≤a<3.
12. 已知集合 $ A = \{ x | x^2 - px - 2 = 0 \} $,$ B = \{ x | x^2 + qx + r = 0 \} $,且 $ A \cup B = \{ - 2,1,5 \} $,$ A \cap B = \{ - 2 \} $,则 $ p + q + r $ 等于(
A.12
B.6
C.- 14
D.- 12
C
)A.12
B.6
C.- 14
D.- 12
答案:
12.C 因为A∩B={−2},
所以−2∈A且−2∈B,将x=−2代入x²−px−2=0,得p=−1,
所以A={1,−2},
因为A∪B={−2,1,5},A∩B={−2},
所以B={−2,5},
所以q=−[(−2)+5]=−3,r=(−2)×5=−10,
所以p+q+r=−14.
所以−2∈A且−2∈B,将x=−2代入x²−px−2=0,得p=−1,
所以A={1,−2},
因为A∪B={−2,1,5},A∩B={−2},
所以B={−2,5},
所以q=−[(−2)+5]=−3,r=(−2)×5=−10,
所以p+q+r=−14.
13. 设集合 $ M = \{ x | - 4 < x < 3 \} $,$ N = \{ x | t + 2 < x < 2t - 1,t \in \mathbf{R} \} $.若 $ M \cap N = N $,则实数 $ t $ 的取值范围为
{t∣t≤3}
.
答案:
13.{t∣t≤3} 由M∩N=N,得N⊆M.
故当N=∅,即t+2≥2t−1,即t≤3时,M∩N=N成立;
当N≠∅时,由图得t+2≥-4,t+2<2t−1,2t−1≤3,
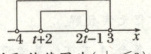
综上可知,所求实数t的取值范围为{t∣t≤3}.
13.{t∣t≤3} 由M∩N=N,得N⊆M.
故当N=∅,即t+2≥2t−1,即t≤3时,M∩N=N成立;
当N≠∅时,由图得t+2≥-4,t+2<2t−1,2t−1≤3,

综上可知,所求实数t的取值范围为{t∣t≤3}.
14. 某网店统计了连续三天售出商品的种类情况:第一天售出 19 种商品,第二天售出 13 种商品,第三天售出 18 种商品;前两天都售出的商品有 3 种,后两天都售出的商品有 4 种.则该网店:
(1) 第一天售出但第二天未售出的商品有
(2) 这三天售出的商品最少有
(1) 第一天售出但第二天未售出的商品有
16
种.(2) 这三天售出的商品最少有
29
种.
答案:
14.
(1)16
(2)29 设三天都售出的商品有x种,第一天售出,第二天
未售出,且第三天售出的商品有y种,则三天售出商品的种类关系
如图所示.
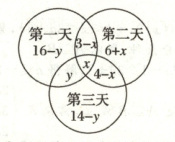
由图可知,
(1)第一天售出但第二天未售出的商品有19−(3−x)−
x=16(种).
(2)这三天售出的商品有(16−y)+y+x+(3−x)+(6+x)+(4−
x)=(43−y)种.
由于{16−y≥0,y≥0,14−y≥0, 所以0≤y≤14.
所以(43−y)_min=43−14=29.
14.
(1)16
(2)29 设三天都售出的商品有x种,第一天售出,第二天
未售出,且第三天售出的商品有y种,则三天售出商品的种类关系
如图所示.

由图可知,
(1)第一天售出但第二天未售出的商品有19−(3−x)−
x=16(种).
(2)这三天售出的商品有(16−y)+y+x+(3−x)+(6+x)+(4−
x)=(43−y)种.
由于{16−y≥0,y≥0,14−y≥0, 所以0≤y≤14.
所以(43−y)_min=43−14=29.
15. 设集合 $ A = \{ 2, - 1,x^2 - x + 1 \} $,$ B = \{ 2y, - 4,x + 4 \} $,$ C = \{ - 1,7 \} $,且 $ A \cap B = C $,求实数 $ x,y $ 的值及 $ A \cup B $.
答案:
15.解 由题意,得7∈A,7∈B且−1∈B,
所以在集合A中x²−x+1=7,
解得x=−2或x=3.
当x=−2时,在集合B中,x+4=2,
又2∈A,故2∈(A∩B)=C,
但2∉C,故x=−2不符合题意,舍去.
当x=3时,在集合B中,x+4=7,
所以2y=−1,解得y=−1/2,符合题意,
所以A={2,−1,7},B={−1,−4,7},
所以A∪B={2,−1,7,−4}.
所以在集合A中x²−x+1=7,
解得x=−2或x=3.
当x=−2时,在集合B中,x+4=2,
又2∈A,故2∈(A∩B)=C,
但2∉C,故x=−2不符合题意,舍去.
当x=3时,在集合B中,x+4=7,
所以2y=−1,解得y=−1/2,符合题意,
所以A={2,−1,7},B={−1,−4,7},
所以A∪B={2,−1,7,−4}.
查看更多完整答案,请扫码查看


