2026年学易优同步学案导学高中数学必修第一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优同步学案导学高中数学必修第一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第230页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
- 第206页
- 第207页
- 第208页
- 第209页
- 第210页
- 第211页
- 第212页
- 第213页
- 第214页
- 第215页
- 第216页
- 第217页
- 第218页
- 第219页
- 第220页
- 第221页
- 第222页
- 第223页
- 第224页
- 第225页
- 第226页
- 第227页
- 第228页
- 第229页
- 第230页
- 第231页
- 第232页
- 第233页
- 第234页
- 第235页
- 第236页
- 第237页
- 第238页
- 第239页
- 第240页
- 第241页
- 第242页
- 第243页
- 第244页
- 第245页
- 第246页
- 第247页
- 第248页
- 第249页
- 第250页
- 第251页
- 第252页
- 第253页
- 第254页
- 第255页
- 第256页
- 第257页
- 第258页
- 第259页
- 第260页
- 第261页
- 第262页
- 第263页
- 第264页
1. 函数 $ f(x) $ 的图象如图所示,则其最大值、最小值分别为(
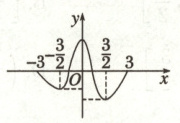
A.$ f(\frac{3}{2}) $,$ f(-\frac{3}{2}) $
B.$ f(0) $,$ f(\frac{3}{2}) $
C.$ f(-\frac{3}{2}) $,$ f(0) $
D.$ f(0) $,$ f(3) $
B
)
A.$ f(\frac{3}{2}) $,$ f(-\frac{3}{2}) $
B.$ f(0) $,$ f(\frac{3}{2}) $
C.$ f(-\frac{3}{2}) $,$ f(0) $
D.$ f(0) $,$ f(3) $
答案:
1.B 观察函数图象可知,$f(x)$的最大值、最小值分别为$f(0)$,$f(\frac{3}{2})$.
2. 设函数 $ f(x)=2x - 1(x \lt 0) $,则 $ f(x) $(
A.有最大值
B.有最小值
C.既有最大值又有最小值
D.既无最大值又无最小值
D
)A.有最大值
B.有最小值
C.既有最大值又有最小值
D.既无最大值又无最小值
答案:
2.D $\because f(x)$在$(-\infty,0)$上单调递增,$\therefore f(x)<f(0)=-1$.
3. 函数 $ f(x)=x^{2}+3x + 2 $ 在区间 $ (-5,5) $ 上的最大值、最小值分别为(
A.$ 42 $,$ 12 $
B.$ 42 $,$ -\frac{1}{4} $
C.$ 12 $,$ -\frac{1}{4} $
D.无最大值,最小值为 $ -\frac{1}{4} $
D
)A.$ 42 $,$ 12 $
B.$ 42 $,$ -\frac{1}{4} $
C.$ 12 $,$ -\frac{1}{4} $
D.无最大值,最小值为 $ -\frac{1}{4} $
答案:
3.D 因为$f(x)=(x+\frac{3}{2})^{2}-\frac{1}{4},x\in(-5,5)$,所以当$x=-\frac{3}{2}$时,$f(x)$有最小值$-\frac{1}{4}$,$f(x)$无最大值.
4. 某公司在甲、乙两地同时销售一种品牌车,利润(单位:万元)分别为 $ L_{1}=-x^{2}+21x $ 和 $ L_{2}=2x $(其中销售量单位:辆)。若该公司在两地共销售 $ 15 $ 辆,则能获得的最大利润为(
A.$ 90 $ 万元
B.$ 60 $ 万元
C.$ 120 $ 万元
D.$ 120.25 $ 万元
C
)A.$ 90 $ 万元
B.$ 60 $ 万元
C.$ 120 $ 万元
D.$ 120.25 $ 万元
答案:
4.C 设公司在甲地销售$x$辆,则在乙地销售$(15 - x)$辆,公司获利为$L=-x^{2}+21x + 2(15 - x)=-x^{2}+19x + 30=-(x-\frac{19}{2})^{2}+30+\frac{19^{2}}{4}$,$\therefore$当$x = 9$或$10$时,$L$最大值为$120$万元.
5. 规定 $ \max\{a,b\} $ 表示取 $ a,b $ 中的较大者,例如 $ \max\{0.1,-2\}=0.1 $,$ \max\{2,2\}=2 $。则函数 $ f(x)=\max\{x + 1,4 - 2x\} $ 的最小值为(
A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $
B
)A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $
答案:
5.B 当$x + 1\geqslant4 - 2x$,即$x\geqslant1$时,$\max(x + 1,4 - 2x)=x + 1$;当$x + 1<4 - 2x$,即$x<1$时,$\max(x + 1,4 - 2x)=4 - 2x$;所以$f(x)=\begin{cases}4 - 2x,x<1,\\x + 1,x\geqslant1,\end{cases}$显然$f(x)$在$(-\infty,1]$上单调递减,在$[1,+\infty)$上单调递增,所以当$x = 1$时,$f(x)$取得最小值为$f(1)=2$.
6. (多选)若函数 $ f(x)=x^{2}-4x + 1 $ 在定义域 $ A $ 上的值域为 $ [-3,1] $,则区间 $ A $ 可能为(
A.$ [0,4] $
B.$ [2,4] $
C.$ [1,4] $
D.$ [-3,5] $
ABC
)A.$ [0,4] $
B.$ [2,4] $
C.$ [1,4] $
D.$ [-3,5] $
答案:
6.ABC $\because$函数$f(x)=x^{2}-4x + 1$的图象是开口向上的抛物线,以直线$x = 2$为对称轴,$\therefore$函数$f(x)$在区间$(-\infty,2)$上单调递减,在$[2,+\infty)$上单调递增.当$x\in[0,4]$时,函数的最小值为$f(2)=-3$,最大值为$f(0)=f(4)=1$,得函数的值域为$[-3,1]$;当$x\in[2,4]$时,函数的最小值为$f(2)=-3$,最大值为$f(4)=1$,得函数的值域为$[-3,1]$;当$x\in[1,4]$时,函数的最小值为$f(2)=-3$,$\because f(1)=-2<f(4)=1$,$\therefore$最大值为$f(4)=1$,得函数的值域为$[-3,1]$;当$x\in[-3,5]$时,最小值为$f(2)=-3$,$\because f(-3)=22>f(5)=6$,$\therefore$最大值为$f(-3)=22$,得函数的值域为$[-3,22]$.根据以上的讨论可得区间$A$不可能为$[-3,5]$.
7. 函数 $ y = ax + 1 $ 在区间 $ [1,3] $ 上的最大值为 $ 4 $,则 $ a = $
1
。
答案:
7.1 若$a<0$,则函数$y = ax + 1$在区间$[1,3]$上单调递减,并且在区间的左端点处取得最大值,即$a + 1 = 4$,解得$a = 3$,不满足$a<0$,舍去;若$a>0$,则函数$y = ax + 1$在区间$[1,3]$上单调递增,并且在区间的右端点处取得最大值,即$3a + 1 = 4$,解得$a = 1$.综上,$a = 1$.
8. 函数 $ f(x)=\frac{1}{x - 3} $,$ x \in [1,2] $,则 $ f(x) $ 的最大值为
$-\frac{1}{2}$
,最小值为$-1$
。
答案:
8.$-\frac{1}{2}$ $-1$ $\because f(x)=\frac{1}{x - 3}$在$[1,2]$上单调递减,$\therefore f(2)\leqslant f(x)\leqslant f(1)$,即$-1\leqslant f(x)\leqslant-\frac{1}{2}$.
9. 画出函数 $ y = -x(|x - 2| - 2) $,$ x \in [-1,5] $ 的图象,并根据图象指出函数的单调区间和最大值、最小值。
答案:
9.解 原函数化为$y=\begin{cases}x^{2},-1\leqslant x\leqslant2,\\-x^{2}+4x,2<x\leqslant5,\end{cases}$在平面直角坐标系内作出其图象,如图
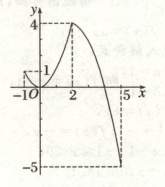
观察图象得,函数$y=-x(|x - 2|-2)$的单调递减区间是$[-1,0]$,$[2,5]$,单调递增区间是$(0,2)$,当$x = 2$时,$y_{\max}=4$,当$x = 5$时,$y_{\min}=-5$,所以原函数最大值为$4$,最小值为$-5$.
9.解 原函数化为$y=\begin{cases}x^{2},-1\leqslant x\leqslant2,\\-x^{2}+4x,2<x\leqslant5,\end{cases}$在平面直角坐标系内作出其图象,如图

观察图象得,函数$y=-x(|x - 2|-2)$的单调递减区间是$[-1,0]$,$[2,5]$,单调递增区间是$(0,2)$,当$x = 2$时,$y_{\max}=4$,当$x = 5$时,$y_{\min}=-5$,所以原函数最大值为$4$,最小值为$-5$.
查看更多完整答案,请扫码查看


