《2026年学易优同步学案导学高中数学必修第一册人教版》

10. (1)已知 $ f(x - \frac{1}{x}) = x^2 + \frac{1}{x^2} $，求 $ f(x) $；
(2)已知函数 $ f(x) = x^2 - bx + c $ 且 $ f(1) = 0 $，$ f(2) = -3 $，求 $ f(x) $.

答案： 10.解
(1)$\because f(x - \frac{1}{x}) = x^2 + \frac{1}{x^2} = (x - \frac{1}{x})^2 + 2$，$\therefore f(x) = x^2 + 2$。
(2) 由$\begin{cases} f(1) = 1 - b + c = 0, \\ f(2) = 4 - 2b + c = -3, \end{cases}$解得$\begin{cases} b = 6, \\ c = 5, \end{cases}$故$f(x) = x^2 - 6x + 5$。

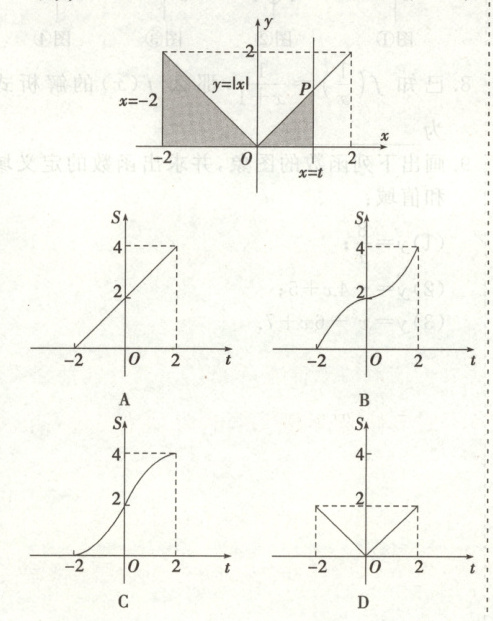
11. 在函数 $ y = |x|(x \in [-2,2]) $ 的图象上有一点 $ P(t,|t|) $，此函数的图象与 $ x $ 轴、直线 $ x = -2 $ 及 $ x = t $ 围成的图形(如图阴影部分)的面积为 $ S $，则 $ S $ 与 $ t $ 的函数关系图象可表示为(B)

答案： 11.B 当$-2 \leq t ＜ 0$时，$S = 2 - \frac{t^2}{2}$，其图象是开口向下的抛物线，顶点坐标是$(0,2)$；当$0 ＜ t \leq 2$时，$S = 2 + \frac{t^2}{2}$，其图象是开口向上的抛物线，顶点坐标是$(0,2)$，所以B满足要求。

12. 若 $ y = f(x + 3) $ 的图象经过点 $ P(1,4) $，则函数 $ y = f(x) $ 的图象必经过点(C)

A.$ (-2,4) $
B.$ (1,1) $
C.$ (4,4) $
D.$ (1,7) $

答案： 12.C 由于点$P(1,4)$在$y = f(x + 3)$的图象上，且$y = f(x)$的图象是由$y = f(x + 3)$的图象向右平移3个单位长度得到的，点$P(1,4)$也向右平移3个单位长度，变成点$(4,4)$，因此$y = f(x)$的图象必经过点$(4,4)$。

13. 已知函数 $ f(x) $ 是一次函数，且 $ f(f(x) - 4x) = 5 $ 恒成立，则 $ f(2) $ 等于(D)

A.$ 1 $
B.$ 3 $
C.$ 7 $
D.$ 9 $

答案： 13.D 因为函数$f(x)$是一次函数，且$f[f(x) - 4x] = 5$恒成立，令$f(x) - 4x = t$，则$f(x) = 4x + t$，所以$f(t) = 4t + t = 5$，解得$t = 1$，所以$f(x) = 4x + 1$，$f(2) = 4 × 2 + 1 = 9$。

14. 已知函数 $ f(x) = \frac{x}{ax + b}(a,b $ 为常数，且 $ a \neq 0) $ 满足 $ f(2) = 1 $，方程 $ f(x) = x $ 有唯一解，则函数 $ f(x) $ 的解析式为$f(x) = \frac{2x}{x + 2}$.

答案： 14.$f(x) = \frac{2x}{x + 2}$ 由$f(x) = x$，得$\frac{x}{ax + b} = x$，即$ax^2 + (b - 1)x = 0$。$\because$方程$f(x) = x$有唯一解，$\therefore \Delta = (b - 1)^2 = 0$，即$b = 1$。$\because f(2) = 1$，$\therefore \frac{2}{2a + b} = 1$，$\therefore a = \frac{1}{2}$。$\therefore f(x) = \frac{x}{\frac{1}{2}x + 1} = \frac{2x}{x + 2}$。

15. 已知函数 $ f(x) = x^2 + (a + 1)x + b $ 满足 $ f(3) = 3 $，且 $ f(x) \geq x $ 恒成立，求 $ f(x) $ 的解析式.

答案： 15.解 由$f(3) = 3$，得$b = -3a - 9$。由$f(x) \geq x$恒成立可知，$x^2 + ax + b \geq 0$恒成立，所以$\Delta = a^2 - 4b \leq 0$，所以$a^2 + 12a + 36 = (a + 6)^2 \leq 0$，所以$a = -6$，$b = 9$。所以$f(x) = x^2 - 5x + 9$。