《2025年新课标同步单元练习九年级数学上册北师大版深圳专版》

1. 梳理本章内容，用适当的方式呈现全章的知识结构.

答案： 本章知识结构如下：
1. 二次函数的定义：
一般形式$y = ax^{2}+bx + c(a\neq0)$。
2. 二次函数的图象：
画法：描点法，列表、描点、连线。
性质：
$a\gt0$，开口向上；$a\lt0$，开口向下。
对称轴$x =-\frac{b}{2a}$。
顶点坐标$(-\frac{b}{2a},\frac{4ac - b^{2}}{4a})$。
3. 二次函数的表达式：
一般式$y = ax^{2}+bx + c(a\neq0)$。
顶点式$y = a(x - h)^{2}+k(a\neq0)$。
交点式$y=a(x - x_{1})(x - x_{2})(a\neq0)$（与$x$轴交点为$(x_1,0)$，$(x_2,0)$）。
4. 二次函数的应用：
利润问题、面积问题等实际情境中二次函数模型的建立与最值求解。

2. 已知四条线段 $ a $，$ b $，$ c $，$ d $ 成比例，且 $ a = 1 $，$ b = 3 $，$ c = 3 $，则 $ d = ($ ).

A.$ 3 $
B.$ 6 $
C.$ 8 $
D.$ 9 $

答案： D

3. 线段 $ AB $ 的长为 $ 2 $，点 $ C $ 是线段 $ AB $ 的黄金分割点，则线段 $ AC $ 的长可能是().

A.$ \sqrt{5} + 1 $
B.$ 2 - \sqrt{5} $
C.$ 3 - \sqrt{5} $
D.$ \sqrt{5} - 2 $

答案： C

4. 如图 4 - 1，$ AB $ 与 $ CD $ 相交于点 $ E $，$ AD // BC $，$ \frac{BE}{AE} = \frac{3}{5} $，$ CD = 16 $，则 $ DE $ 的长为.

 

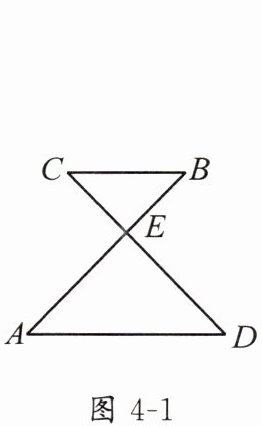
答案： 10

5. 《九章算术》中记载了一种测量井深的方法. 如图 4 - 2，在井口 $ B $ 处立一根垂直于井口的木杆 $ BD $，从木杆的顶端 $ D $ 观察井水水岸 $ C $，视线 $ DC $ 与井口的直径 $ AB $ 交于点 $ E $，如果测得 $ AB = 1.6 \, m $，$ BD = 1 \, m $，$ BE = 0.2 \, m $，那么 $ AC = $$ m $.

答案： 7

6. 如图 4 - 3，$ CE $ 是平行四边形 $ ABCD $ 的边 $ AB $ 的垂直平分线，垂足为点 $ O $，$ CE $ 与 $ DA $ 的延长线交于点 $ E $. 连接 $ AC $，$ BE $，$ DO $，$ DO $ 与 $ AC $ 交于点 $ F $，给出下列结论：① 四边形 $ ACBE $ 是菱形；② $ \angle ACD = \angle BAE $；③ $ AF : BE = 2 : 3 $；④ $ S_{四边形AFOE} : S_{\triangle COD} = 2 : 3 $. 其中正确的结论有.(填序号)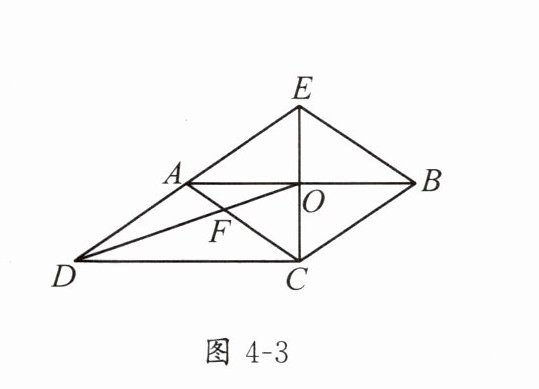

答案： ①②④ 解析：因为四边形 ABCD 是平行四边形，
所以 AB//CD，AB=CD.
因为 EC 垂直平分 AB，
所以 OA=OB=$\frac{1}{2}$AB=$\frac{1}{2}$DC，CD⊥CE.
因为 OA//DC，
所以$\frac{EA}{ED}$=$\frac{EO}{EC}$=$\frac{OA}{CD}$=$\frac{1}{2}$，
所以 AE=AD，OE=OC.
因为 OA=OB，OE=OC，
所以四边形 ACBE 是平行四边形.
因为 AB⊥EC，
所以四边形 ACBE 是菱形，故①正确.
因为∠DCE=90°，DA=AE，
所以 AC=AD=AE，
所以∠ACD=∠ADC.
因为 AB//DC，
所以∠ADC=∠BAE，
所以∠ACD=∠BAE，故②正确.
因为 OA//CD，
所以$\frac{AF}{CF}$=$\frac{OA}{CD}$=$\frac{1}{2}$，
所以$\frac{AF}{AC}$=$\frac{AF}{BE}$=$\frac{1}{3}$，故③错误.
设△AOF 的面积为 a，则△OFC 的面积为 2a，
△CDF 的面积为 4a，△AOC 的面积=△AOE 的面积=3a，
所以四边形 AFOE 的面积为 4a，
△ODC 的面积为 6a，
所以$S_{四边形AFOE}:S_{\triangle COD}$=2:3，故④正确.