第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
2. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用.
例:已知$x$可取任何实数,试求二次三项式$x²+6x-1$的最小值.
解:$x²+6x-1=x²+2×3x+3²-3²-1=(x+3)²-10$.
因为无论$x$取何实数,总有$(x+3)²≥0$.
所以$(x+3)²-10≥-10$,即$x²+6x-1$的最小值是-10,
即无论$x$取何实数,$x²+6x-1$的值总是不小于-10的实数.
问题:
(1)已知$y=x²-4x+7$,求证:$y$是正数.
知识迁移:
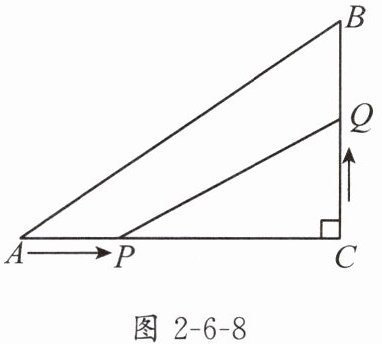
(2)如图2-6-8,在Rt△ABC中,$\angle C=90°$,$AC=6$cm,$BC=4$cm,点P在边AC上,从点A向点C以2cm/s的速度移动,点Q在边CB上,从点C向点B以$\sqrt{3}$cm/s的速度移动.若点P,Q同时出发,且当一点移动到终点时停止移动,另一点也随之停止移动.设△PCQ的面积为$S$cm²,运动时间为$t$s,求$S$的最大值.
例:已知$x$可取任何实数,试求二次三项式$x²+6x-1$的最小值.
解:$x²+6x-1=x²+2×3x+3²-3²-1=(x+3)²-10$.
因为无论$x$取何实数,总有$(x+3)²≥0$.
所以$(x+3)²-10≥-10$,即$x²+6x-1$的最小值是-10,
即无论$x$取何实数,$x²+6x-1$的值总是不小于-10的实数.
问题:
(1)已知$y=x²-4x+7$,求证:$y$是正数.
知识迁移:
(2)如图2-6-8,在Rt△ABC中,$\angle C=90°$,$AC=6$cm,$BC=4$cm,点P在边AC上,从点A向点C以2cm/s的速度移动,点Q在边CB上,从点C向点B以$\sqrt{3}$cm/s的速度移动.若点P,Q同时出发,且当一点移动到终点时停止移动,另一点也随之停止移动.设△PCQ的面积为$S$cm²,运动时间为$t$s,求$S$的最大值.

答案:
(1)证明:$y=x^{2}-4x+7=x^{2}-4x+4+3=(x-2)^{2}+3$.
因为$(x-2)^{2}\geqslant0$,
所以$y\geqslant0+3=3$. 所以$y>0$. 所以y是正数.
(2)解:由题意得$AP=2t cm$,$CQ=\sqrt{3}t cm$,$PC=(6-2t)cm(0<t\leqslant\frac{4\sqrt{3}}{3})$.
所以$S=\frac{1}{2}PC\cdot CQ$
$=\frac{1}{2}(6-2t)\cdot\sqrt{3}t$
$=-\sqrt{3}t^{2}+3\sqrt{3}t$
$=-\sqrt{3}(t^{2}-3t)$
$=-\sqrt{3}(t-\frac{3}{2})^{2}+\frac{9\sqrt{3}}{4}$.
因为$(t-\frac{3}{2})^{2}\geqslant0$,
所以当$t=\frac{3}{2}$时,S取得最大值$\frac{9\sqrt{3}}{4}$.
(1)证明:$y=x^{2}-4x+7=x^{2}-4x+4+3=(x-2)^{2}+3$.
因为$(x-2)^{2}\geqslant0$,
所以$y\geqslant0+3=3$. 所以$y>0$. 所以y是正数.
(2)解:由题意得$AP=2t cm$,$CQ=\sqrt{3}t cm$,$PC=(6-2t)cm(0<t\leqslant\frac{4\sqrt{3}}{3})$.
所以$S=\frac{1}{2}PC\cdot CQ$
$=\frac{1}{2}(6-2t)\cdot\sqrt{3}t$
$=-\sqrt{3}t^{2}+3\sqrt{3}t$
$=-\sqrt{3}(t^{2}-3t)$
$=-\sqrt{3}(t-\frac{3}{2})^{2}+\frac{9\sqrt{3}}{4}$.
因为$(t-\frac{3}{2})^{2}\geqslant0$,
所以当$t=\frac{3}{2}$时,S取得最大值$\frac{9\sqrt{3}}{4}$.
3. 子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”——《论语·第二章·为政篇》
列方程解决下面问题:
读诗词解题(通过列方程式,算出周瑜去世时的年龄):
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
列方程解决下面问题:
读诗词解题(通过列方程式,算出周瑜去世时的年龄):
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
答案:
解:设周瑜去世时的年龄的个位数字为x,则十位数字为$x-3$,
根据题意得$10(x-3)+x=x^{2}$,
解得$x_{1}=5$,$x_{2}=6$.
当$x=5$时,周瑜的年龄是25岁,
因为25非而立之年,
所以不符合题意,舍去;
当$x=6$时,周瑜的年龄是36岁,符合题意.
答:周瑜去世时的年龄是36岁.
根据题意得$10(x-3)+x=x^{2}$,
解得$x_{1}=5$,$x_{2}=6$.
当$x=5$时,周瑜的年龄是25岁,
因为25非而立之年,
所以不符合题意,舍去;
当$x=6$时,周瑜的年龄是36岁,符合题意.
答:周瑜去世时的年龄是36岁.
查看更多完整答案,请扫码查看


