第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 如图1-7,在菱形 $ABCD$ 中,$\angle BAD = 120^{\circ}$,$AB = 4$,$E$,$F$ 分别是 $AB$,$AD$ 上的动点且 $BE = AF$,给出下列结论:① $\triangle BEC\cong\triangle AFC$;② $\triangle ECF$ 为等边三角形;③ $\angle AGE = \angle AFC$. 其中正确结论的序号有
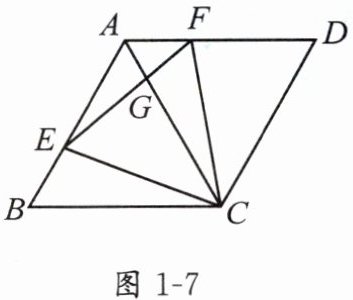
①②③
.
答案:
①②③
2. 如图1-8①,$\mathrm{Rt}\triangle CEF$ 中,$\angle C = 90^{\circ}$,$\angle CEF$,$\angle CFE$ 处的外角平分线交于点 $A$,过点 $A$ 分别作直线 $CE$,$CF$ 的垂线,$B$,$D$ 为垂足.
(1) $\angle EAF=$
(2)①求证:四边形 $ABCD$ 是正方形;
②若 $BE = EC = 3$,求 $DF$ 的长.
(3)如图1-8②,在 $\triangle PQR$ 中,$\angle QPR = 45^{\circ}$,高 $PH = 5$,$QH = 2$,则 $HR$ 的长为

(1) $\angle EAF=$
45
$^{\circ}$.(2)①求证:四边形 $ABCD$ 是正方形;
②若 $BE = EC = 3$,求 $DF$ 的长.
(3)如图1-8②,在 $\triangle PQR$ 中,$\angle QPR = 45^{\circ}$,高 $PH = 5$,$QH = 2$,则 $HR$ 的长为
$\frac{15}{7}$
.
答案:
(1)45
(2)①证明: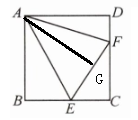 ,则∠AGE=∠AGF=90°.因为 AB⊥CE,AD⊥CF,所以∠B=∠D=90°=∠C,所以四边形 ABCD 是矩形.因为∠CEF,∠CFE 处的外角平分线交于点 A,所以 AB=AG,AD=AG,所以 AB=AD,所以四边形 ABCD 是正方形.
,则∠AGE=∠AGF=90°.因为 AB⊥CE,AD⊥CF,所以∠B=∠D=90°=∠C,所以四边形 ABCD 是矩形.因为∠CEF,∠CFE 处的外角平分线交于点 A,所以 AB=AG,AD=AG,所以 AB=AD,所以四边形 ABCD 是正方形.
②解:设 DF=x,因为 BE=EC=3,所以 BC=6.由①得四边形 ABCD 是正方形,所以 BC=CD=6.在 Rt△ABE 与 Rt△AGE 中,$\begin{cases} AB=AG, \\ AE=AE, \end{cases}$所以 Rt△ABE≌Rt△AGE(HL),所以 BE=EG=3,同理,GF=DF=x.在 Rt△CEF 中,EC²+FC²=EF²,即 3²+(6 - x)²=(x + 3)²,解得 x=2,所以 DF 的长为 2.
(3)$\frac{15}{7}$
(1)45
(2)①证明:
 ,则∠AGE=∠AGF=90°.因为 AB⊥CE,AD⊥CF,所以∠B=∠D=90°=∠C,所以四边形 ABCD 是矩形.因为∠CEF,∠CFE 处的外角平分线交于点 A,所以 AB=AG,AD=AG,所以 AB=AD,所以四边形 ABCD 是正方形.
,则∠AGE=∠AGF=90°.因为 AB⊥CE,AD⊥CF,所以∠B=∠D=90°=∠C,所以四边形 ABCD 是矩形.因为∠CEF,∠CFE 处的外角平分线交于点 A,所以 AB=AG,AD=AG,所以 AB=AD,所以四边形 ABCD 是正方形.②解:设 DF=x,因为 BE=EC=3,所以 BC=6.由①得四边形 ABCD 是正方形,所以 BC=CD=6.在 Rt△ABE 与 Rt△AGE 中,$\begin{cases} AB=AG, \\ AE=AE, \end{cases}$所以 Rt△ABE≌Rt△AGE(HL),所以 BE=EG=3,同理,GF=DF=x.在 Rt△CEF 中,EC²+FC²=EF²,即 3²+(6 - x)²=(x + 3)²,解得 x=2,所以 DF 的长为 2.
(3)$\frac{15}{7}$
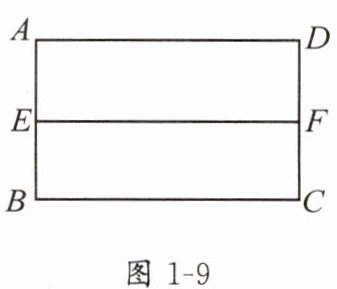
3. 如图1-9,在矩形 $ABCD$ 中,$AB = 5$,$BC = 8$,$E$,$F$ 分别为 $AB$,$CD$ 的中点.
(1)求证:四边形 $AEFD$ 是矩形.
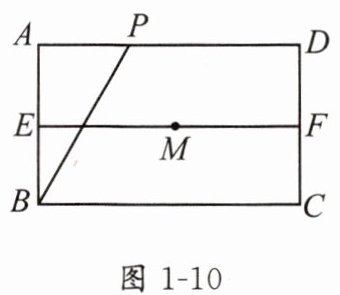
(2)如图1-10,点 $P$ 是边 $AD$ 上一点,点 $A$ 关于 $BP$ 的对称点为点 $M$.
①当点 $M$ 落在线段 $EF$ 上时,$\angle ABP=$
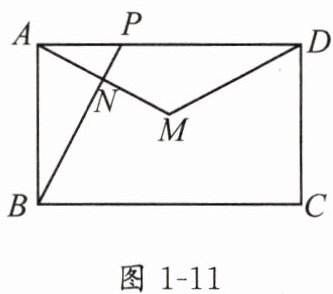
②如图1-11,连接 $AM$ 交 $BP$ 于点 $N$,连接 $DM$,当 $\triangle AMD$ 是等腰三角形时,直接写出 $AN$ 的长.
(1)求证:四边形 $AEFD$ 是矩形.
(2)如图1-10,点 $P$ 是边 $AD$ 上一点,点 $A$ 关于 $BP$ 的对称点为点 $M$.
①当点 $M$ 落在线段 $EF$ 上时,$\angle ABP=$
30°
;②如图1-11,连接 $AM$ 交 $BP$ 于点 $N$,连接 $DM$,当 $\triangle AMD$ 是等腰三角形时,直接写出 $AN$ 的长.



答案:
(1)证明:因为四边形 ABCD 是矩形,所以 AB=CD,AB//CD,∠A=90°.因为 E,F 分别为 AB,CD 的中点,所以 AE=EB,DF=FC,所以 AE=DF,AE//DF,所以四边形 AEFD 是平行四边形.因为∠A=90°,所以平行四边形 AEFD 是矩形.
(2)解:①30°
②AN 的长为$\sqrt{5}$或 4 或$\frac{40\sqrt{89}}{89}$.
(1)证明:因为四边形 ABCD 是矩形,所以 AB=CD,AB//CD,∠A=90°.因为 E,F 分别为 AB,CD 的中点,所以 AE=EB,DF=FC,所以 AE=DF,AE//DF,所以四边形 AEFD 是平行四边形.因为∠A=90°,所以平行四边形 AEFD 是矩形.
(2)解:①30°
②AN 的长为$\sqrt{5}$或 4 或$\frac{40\sqrt{89}}{89}$.
查看更多完整答案,请扫码查看


