《2025年新课标同步单元练习九年级数学上册北师大版深圳专版》

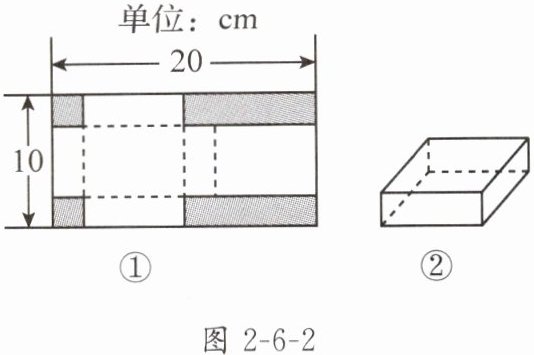
2. 如图2-6-2①，将一张长20cm、宽10cm的矩形硬纸片裁剪掉图中阴影部分之后，恰好折成如图2-6-2②所示的有盖纸盒，纸盒底面积为48cm²，则该有盖纸盒的高为(C).

A.4 cm
B.3 cm
C.2 cm
D.1 cm

答案： C 解析：设该纸盒的高为x cm. 依题意，得
$\frac{20-2x}{2}×(10-2x)=48$，
化简，得$x^{2}-15x+26=0$，
解得$x_{1}=2$，$x_{2}=13$.
当$x=2$时，$10-2x=6＞0$，符合题意；
当$x=13$时，$10-2x=-16＜0$，不符合题意，舍去.

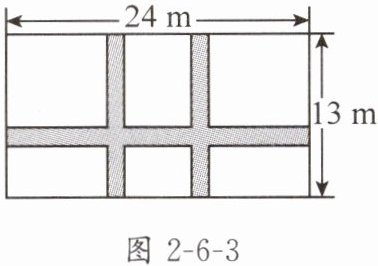
3. 如图2-6-3，在宽为13m、长为24m的矩形场地上修建同样宽的三条小路(横向与纵向垂直)，其余部分种草坪，假设草坪面积为264m²，求小路的宽为多少.设小路的宽为$x$m，则列出的方程是(13-x)(24-2x)=264.

答案： $(13-x)(24-2x)=264$

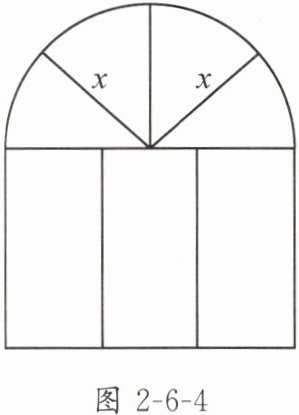
4. 某建筑物的窗户如图2-6-4所示，它的上半部分的形状是半圆，半径为$x$m，下半部分的形状是矩形，制造窗框的材料总长（图中所有黑线的长度和）为15m.当$x$等于多少时，窗户的面积是4m²？

答案： 解：由题可知，矩形的长为$2x$ m，设矩形的宽为y m.
因为制造窗框的材料总长为15 m，
所以$y=\frac{15-7x-\pi x}{4}$.
依题意得$\frac{1}{2}\pi x^{2}+2xy=4$，
即$\frac{1}{2}\pi x^{2}+2x\cdot \frac{15-7x-\pi x}{4}=4$，
整理得$7x^{2}-15x+8=0$，
解得$x_{1}=1$，$x_{2}=\frac{8}{7}$.
答：当x等于1或$\frac{8}{7}$时，窗户的面积是$4m^{2}$.

5. 如图2-6-5，利用一面墙(墙长25m)，用总长度为49m的栅栏(图中实线部分)围成一个矩形围栏ABCD，且中间共留两个1m宽的小门，设栅栏BC的长为$x$m.
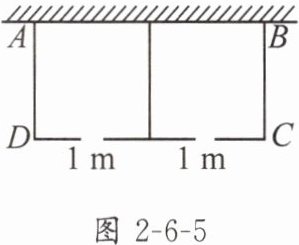
(1)$AB=$(51-3x)m(用含$x$的代数式表示).
(2)若矩形围栏ABCD的面积为210m²，求栅栏BC的长.
(3)矩形围栏ABCD的面积是否有可能达到240m²？若有可能，求出相应$x$的值；若不可能，说明理由.

答案：
(1)$(51-3x)$ 解析：因为栅栏的全长为49 m，且中间共留两个1 m宽的小门，
所以$AB=49-3x+2=51-3x(m)$.
(2)依题意，得$(51-3x)x=210$，
整理，得$x^{2}-17x+70=0$，
解得$x_{1}=7$，$x_{2}=10$.
当$x=7$时，$AB=51-3x=30＞25$，不合题意，舍去；
当$x=10$时，$AB=51-3x=21＜25$，符合题意.
故栅栏BC的长为10 m.
(3)不可能. 理由如下：
依题意，得$(51-3x)x=240$，
整理，得$x^{2}-17x+80=0$，
因为$\Delta=(-17)^{2}-4×1×80=-31＜0$，
所以该方程没有实数根，
所以矩形围栏ABCD的面积不可能达到$240m^{2}$.