《2025年新课标同步单元练习九年级数学上册北师大版深圳专版》

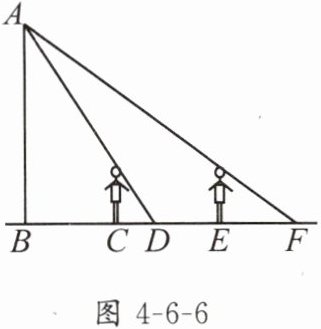
1. 如图4-6-6，王华晚上由路灯A下的B处走到C处时，测得影子CD的长为1m，继续往前走3m到达E处时，影子EF的长为2m，已知王华的身高是1.5m，那么路灯A的高度AB为6m.

答案： 6

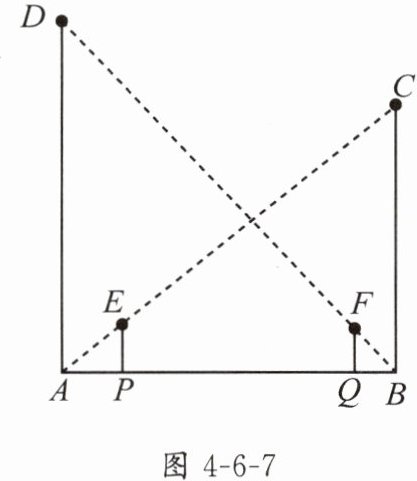
2. 如图4-6-7，D，C为两路灯，身高相同的小明、小亮站在两路灯杆AD，BC之间，两人相距6.5m，小明站在P处，小亮站在Q处，小明在路灯C下的影长为2m，已知小明身高1.8m，路灯杆BC高9m.小明在路灯C下的影子顶部恰好位于路灯D的正下方，小亮在路灯D下的影子顶部恰好位于路灯C的正下方.
(1)计算小亮在路灯D下的影长；
(2)计算路灯杆AD的高.

答案：
(1)因为 EP⊥AB，CB⊥AB，
所以∠EPA=∠CBA=90°.
因为∠EAP=∠CAB，
所以△EAP∽△CAB，
所以$\frac{EP}{BC}=\frac{AP}{AB}$，
所以$\frac{1.8}{9}=\frac{2}{AB}$，
所以 AB=10，
所以 BQ=10-2-6.5=1.5.
由题意知，小亮在路灯 D 下的影子为 BQ，
故小亮在路灯 D 下的影长为 1.5 m.
(2)因为 FQ⊥AB，DA⊥AB，
所以∠FQB=∠DAB=90°.
因为∠FBQ=∠DBA，
所以△BFQ∽△BDA，
所以$\frac{FQ}{DA}=\frac{BQ}{AB}$，
所以$\frac{1.8}{DA}=\frac{1.5}{10}$，
所以 DA=12.
故路灯杆 AD 的高为 12 m.

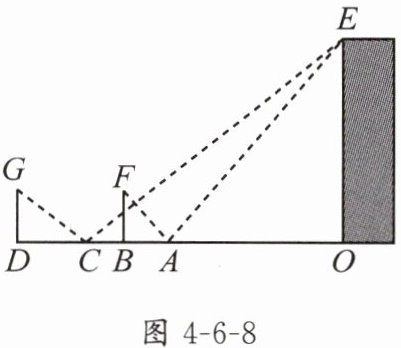
3. 如图4-6-8，为了测量一栋楼OE的高度，小明同学先在操场上A处放一面镜子，向后退到B处，恰好在镜子中看到楼的顶部E；再将镜子放到C处，然后后退到D处，恰好再次在镜子中看到楼的顶部E(O，A，B，C，D在同一条直线上)，测得AC=2m，BD=2.1m，如果小明眼睛距地面的高度BF，DG均为1.6m，试确定楼OE的高度.

答案： 解：设 OE=a m，AO=b m，CB=x m.
易证得△GDC∽△EOC，所以$\frac{GD}{EO}=\frac{CD}{OC}$，
即$\frac{1.6}{a}=\frac{2.1-x}{2+b}$，
整理得 3.2+1.6b=2.1a-ax①，
易证得△FBA∽△EOA，所以$\frac{FB}{EO}=\frac{AB}{OA}$，
即$\frac{1.6}{a}=\frac{2-x}{b}$，
整理得 1.6b=2a-ax②，
将②代入①得 3.2+2a-ax=2.1a-ax，
所以 a=32，
即 OE=32 m，
故楼 OE 的高度为 32 m.