第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 已知平行四边形 $ABCD$,下列条件中,不能判定这个平行四边形为菱形的是(
A.$AC\perp BD$
B.$\angle ABD=\angle ADB$
C.$AB = CD$
D.$AB = BC$
C
).A.$AC\perp BD$
B.$\angle ABD=\angle ADB$
C.$AB = CD$
D.$AB = BC$
答案:
C
2. 如图 1-1-6,已知四边形 $ABCD$ 的对角线互相垂直,如果适当添加一个条件,就能判定该四边形是菱形,那么这个条件可以是(
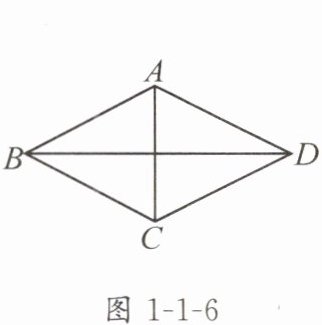
A.$BA = BC$
B.$AC = BD$
C.$AB// CD$
D.$AC$,$BD$ 互相平分
]
D
).
A.$BA = BC$
B.$AC = BD$
C.$AB// CD$
D.$AC$,$BD$ 互相平分
]
答案:
D
3. 如图 1-1-7,小聪在作线段 $AB$ 的垂直平分线时,他是这样操作的:分别以 $A$ 和 $B$ 为圆心,大于 $\frac{1}{2}AB$ 的长为半径画弧,两弧相交于 $C$,$D$,则直线 $CD$ 为所求.根据他的作图方法可知四边形 $ADBC$ 一定是(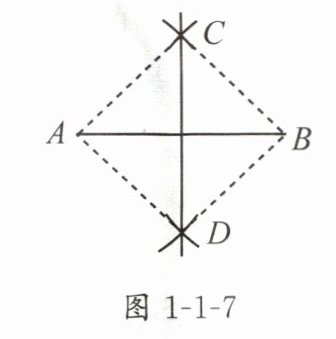
A.矩形
B.菱形
C.正方形
D.等腰梯形
B
).
A.矩形
B.菱形
C.正方形
D.等腰梯形
答案:
B
4. 如图 1-1-8,在四边形 $ABCD$ 中,$E$,$F$ 分别是线段 $AD$,$BC$ 的中点,$G$,$H$ 分别是线段 $BD$,$AC$ 的中点,当四边形 $ABCD$ 的边满足
AB=CD
时,四边形 $EGFH$ 是菱形.
答案:
AB=CD
5. 证明:对角线互相垂直的平行四边形是菱形.
答案:
解:已知:如答图1−1−3,在平行四边形ABCD 中,AC,BD为对角线,相交于点O,且AC⊥BD.求证:四边形ABCD是菱形.
证明:因为四边形ABCD为平行四边形,
所以OA=OC.
又因为AC⊥BD,
所以AB=CB,
所以平行四边形ABCD是菱形.

解:已知:如答图1−1−3,在平行四边形ABCD 中,AC,BD为对角线,相交于点O,且AC⊥BD.求证:四边形ABCD是菱形.
证明:因为四边形ABCD为平行四边形,
所以OA=OC.
又因为AC⊥BD,
所以AB=CB,
所以平行四边形ABCD是菱形.

查看更多完整答案,请扫码查看


