第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 已知不等式组$\left\{\begin{array}{l}3x + 4 > x,①\\ \frac{4}{3}x \leq x + \frac{2}{3}.②\end{array}\right.$
(1)求不等式组的解集,并写出它的所有整数解;
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
(1)求不等式组的解集,并写出它的所有整数解;
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
答案:
(1)由①得$x > -2$,由②得$x\leqslant 2$,
所以不等式组的解集为$-2 < x\leqslant 2$,
所以它的所有整数解为 -1,0,1,2.
(2)如答表 3-1-3
答表 3-1-3
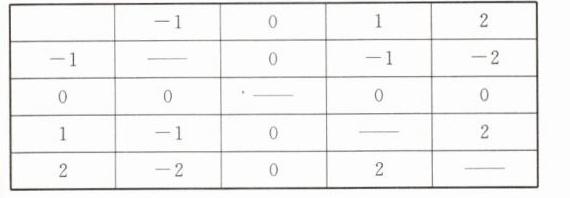
因为共有 12 种等可能的结果,积为正数的有 2 种结果,所以积为正数的概率为$\frac{1}{6}$.
(1)由①得$x > -2$,由②得$x\leqslant 2$,
所以不等式组的解集为$-2 < x\leqslant 2$,
所以它的所有整数解为 -1,0,1,2.
(2)如答表 3-1-3
答表 3-1-3

因为共有 12 种等可能的结果,积为正数的有 2 种结果,所以积为正数的概率为$\frac{1}{6}$.
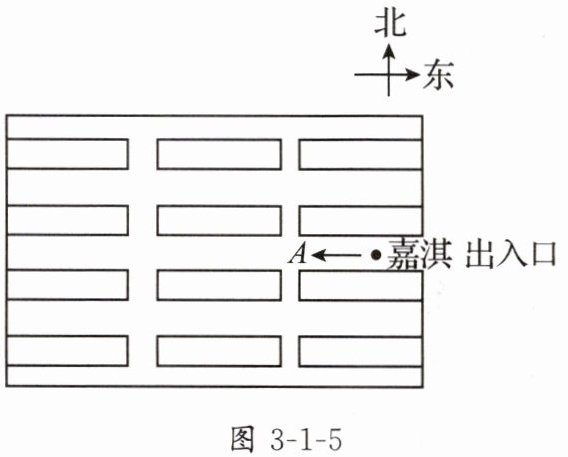
2. 某博物馆展厅的平面图如图3 - 1 - 5所示.嘉淇进入展厅后开始自由参观,每走到一个十字道口,她可能直行,也可能向左转、向右转,且这三种可能性均相同.
(1)求嘉淇走到十字道口A向北走的概率;
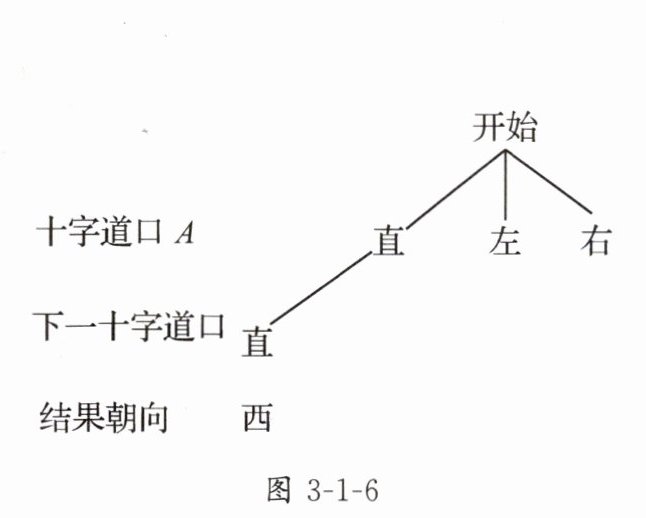
(2)补全图3 - 1 - 6中的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率最大.
(1)求嘉淇走到十字道口A向北走的概率;
(2)补全图3 - 1 - 6中的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率最大.


答案:
(1)向北走的概率为$\frac{1}{3}$.
(2)补全树状图,如答图 3-1-10 所示.

因为共有 9 种等可能的结果,嘉淇经过两个十字道口后向西参观的结果有 3 种,向南参观的结果有 2 种,向北参观的结果有 2 种,向东参观的结果有 2 种,所以向西参观的概率为$\frac{1}{3}$,
向南参观的概率 = 向北参观的概率 = 向东参观的概率 =$\frac{2}{9}$,
所以向西参观的概率最大.
(1)向北走的概率为$\frac{1}{3}$.
(2)补全树状图,如答图 3-1-10 所示.

因为共有 9 种等可能的结果,嘉淇经过两个十字道口后向西参观的结果有 3 种,向南参观的结果有 2 种,向北参观的结果有 2 种,向东参观的结果有 2 种,所以向西参观的概率为$\frac{1}{3}$,
向南参观的概率 = 向北参观的概率 = 向东参观的概率 =$\frac{2}{9}$,
所以向西参观的概率最大.
查看更多完整答案,请扫码查看


