第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
7. 若方程 $ x^{2}-3x - 1 = 0 $ 的两根分别为 $ x_{1} $,$ x_{2} $,则 $ \frac{1}{x_{1}}+\frac{1}{x_{2}} $ 的值为
-3
.
答案:
-3
1. 在解关于 $ x $ 的方程 $ x^{2}+bx + c = 0 $ 时,甲看错了一次项系数,解得两实数根为 $ -1 $ 和 $ 6 $;乙看错了常数项,解得两实数根为 $ -3 $ 和 $ 4 $,求正确的方程.
答案:
解:因为甲看错了一次项系数,解得两根为-1和6,
所以二次项系数和常数项正确.
由$x_{1}\cdot x_{2}=\frac{c}{a}$,得$-1×6=c$,
所以$c=-6$.
因为乙看错了常数项,解得两根为-3和4,
所以二次项系数和一次项系数正确.
由$x_{1}+x_{2}=-\frac{b}{a}$,得$-3+4=-b$,
所以$b=-1$.
所以正确的方程是$x^{2}-x-6=0$.
所以二次项系数和常数项正确.
由$x_{1}\cdot x_{2}=\frac{c}{a}$,得$-1×6=c$,
所以$c=-6$.
因为乙看错了常数项,解得两根为-3和4,
所以二次项系数和一次项系数正确.
由$x_{1}+x_{2}=-\frac{b}{a}$,得$-3+4=-b$,
所以$b=-1$.
所以正确的方程是$x^{2}-x-6=0$.
2. 已知 $ x_{1} $,$ x_{2} $ 是关于 $ x $ 的一元二次方程 $ x^{2}-2(m + 1)x + m^{2}+5 = 0 $ 的两实数根.
(1)若 $ (x_{1}-1)(x_{2}-1)=28 $,求 $ m $ 的值;
(2)已知等腰三角形 $ ABC $ 的一边长为 $ 7 $,若 $ x_{1} $,$ x_{2} $ 恰好是 $ \triangle ABC $ 另外两边的长,求这个三角形的周长.
(1)若 $ (x_{1}-1)(x_{2}-1)=28 $,求 $ m $ 的值;
(2)已知等腰三角形 $ ABC $ 的一边长为 $ 7 $,若 $ x_{1} $,$ x_{2} $ 恰好是 $ \triangle ABC $ 另外两边的长,求这个三角形的周长.
答案:
(1)根据题意得$\Delta=4(m+1)^{2}-4(m^{2}+5)\geq0$,解得$m\geq2$.
$x_{1}+x_{2}=2(m+1)$,$x_{1}x_{2}=m^{2}+5$.
因为$(x_{1}-1)(x_{2}-1)=28$,
即$x_{1}x_{2}-(x_{1}+x_{2})+1=28$,
所以$m^{2}+5-2(m+1)+1=28$,
整理得$m^{2}-2m-24=0$,
解得$m_{1}=6$,$m_{2}=-4$,而$m\geq2$,
所以$m$的值为6.
(2)当腰长为7时,$x=7$是一元二次方程$x^{2}-2(m+1)x+m^{2}+5=0$的一个解,
把$x=7$代入方程得$49-14(m+1)+m^{2}+5=0$,
整理得$m^{2}-14m+40=0$,
解得$m_{1}=10$,$m_{2}=4$.
当$m=10$时,$x_{1}+x_{2}=2(m+1)=22$,解得$x_{2}=15$,而$7+7<15$,故舍去;
当$m=4$时,$x_{1}+x_{2}=2(m+1)=10$,解得$x_{2}=3$,则这个三角形的周长为$3+7+7=17$.
当7为等腰三角形的底边长时,$x_{1}=x_{2}$,所以$\Delta=0$,则$m=2$,
原方程化为$x^{2}-6x+9=0$,
解得$x_{1}=x_{2}=3$,
而$3+3<7$,故舍去.
所以这个三角形的周长为17.
$x_{1}+x_{2}=2(m+1)$,$x_{1}x_{2}=m^{2}+5$.
因为$(x_{1}-1)(x_{2}-1)=28$,
即$x_{1}x_{2}-(x_{1}+x_{2})+1=28$,
所以$m^{2}+5-2(m+1)+1=28$,
整理得$m^{2}-2m-24=0$,
解得$m_{1}=6$,$m_{2}=-4$,而$m\geq2$,
所以$m$的值为6.
(2)当腰长为7时,$x=7$是一元二次方程$x^{2}-2(m+1)x+m^{2}+5=0$的一个解,
把$x=7$代入方程得$49-14(m+1)+m^{2}+5=0$,
整理得$m^{2}-14m+40=0$,
解得$m_{1}=10$,$m_{2}=4$.
当$m=10$时,$x_{1}+x_{2}=2(m+1)=22$,解得$x_{2}=15$,而$7+7<15$,故舍去;
当$m=4$时,$x_{1}+x_{2}=2(m+1)=10$,解得$x_{2}=3$,则这个三角形的周长为$3+7+7=17$.
当7为等腰三角形的底边长时,$x_{1}=x_{2}$,所以$\Delta=0$,则$m=2$,
原方程化为$x^{2}-6x+9=0$,
解得$x_{1}=x_{2}=3$,
而$3+3<7$,故舍去.
所以这个三角形的周长为17.
3. 已知一个直角三角形的两条直角边的长恰好是关于 $ x $ 的方程 $ 2x^{2}+kx + 7 = 0 $ 的两个根,且这个直角三角形的斜边长是 $ 3 $,求 $ k $ 的值.
答案:
解:设直角三角形的斜边长为$c$,两直角边长分别为$a$与$b$,则$c=3$.
因为直角三角形的两条直角边的长恰好是方程$2x^{2}+kx+7=0$的两个根,所以$\Delta=k^{2}-4×2×7>0$,即$k^{2}>56$,
所以$a+b=-\frac{k}{2}$,$ab=3.5$.
根据勾股定理可得$c^{2}=a^{2}+b^{2}=(a+b)^{2}-2ab=\frac{k^{2}}{4}-7=9$,
所以$k=\pm8$.
因为$a+b=-\frac{k}{2}>0$,
所以$k<0$,所以$k=-8$.
因为直角三角形的两条直角边的长恰好是方程$2x^{2}+kx+7=0$的两个根,所以$\Delta=k^{2}-4×2×7>0$,即$k^{2}>56$,
所以$a+b=-\frac{k}{2}$,$ab=3.5$.
根据勾股定理可得$c^{2}=a^{2}+b^{2}=(a+b)^{2}-2ab=\frac{k^{2}}{4}-7=9$,
所以$k=\pm8$.
因为$a+b=-\frac{k}{2}>0$,
所以$k<0$,所以$k=-8$.
1. 如图2-6-1,一艘轮船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报.某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区.当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过(
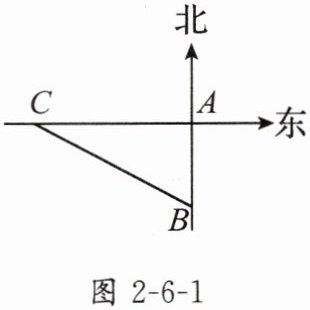
A.10
B.7
C.6
D.12
B
)h它就会进入台风影响区.
A.10
B.7
C.6
D.12
答案:
B
查看更多完整答案,请扫码查看


