《2025年新课标同步单元练习九年级数学上册北师大版深圳专版》

7. 已知关于 $ x $ 的方程 $ x^{2}-mx+(m - 2)=0 $.
(1) 求证：不论 $ m $ 为何值，该方程总有两个不相等的实数根；
(2) 若方程有一个根是 $ 2 $，求 $ m $ 的值以及方程的另一个根.

答案：
(1)证明：因为 a=1，b=-m，c=m-2，所以$\Delta =b^{2}-4ac=(-m)^{2}-4×1×(m-2)=m^{2}-4m+8=(m-2)^{2}+4$。因为$(m-2)^{2}\geq0$，所以$(m-2)^{2}+4＞0$，即$\Delta ＞0$，所以不论 m 为何值，该方程都有两个不相等的实数根。
(2)解：设方程的另一个根为 t，根据题意得，2+t=m，2t=m-2，所以 2+t-2t=2，解得 t=0，所以 m=2，所以 m 的值为 2，另一个根为 0。

1. 如图 2 - 2，一根木棍 $ OE $ 垂直平分柱子 $ AB $，$ AB = 200 $ cm，$ OE = 260 $ cm，一只小猫 $ C $ 由柱子底端 $ A $ 点以 $ 2 $ cm/s 的速度沿柱子 $ AB $ 向顶端 $ B $ 点爬行，同时，另一只小猫 $ D $ 由点 $ O $ 以 $ 3 $ cm/s 的速度沿木棍 $ OE $ 爬行，小猫 $ C $ 爬到顶端 $ B $ 点后，停止爬行，小猫 $ D $ 也随之停止爬行.问：是否存在某一时刻，使以这两只小猫所在位置与点 $ O $ 为顶点的三角形的面积是 $ 1800 $ $ cm^{2} $? (小猫的位置可视为一点)

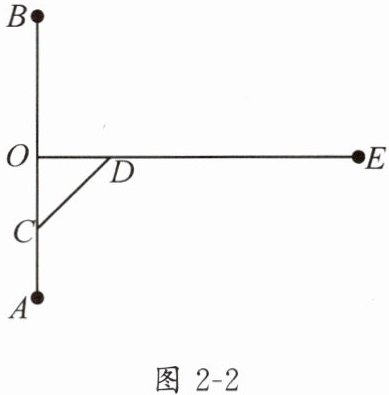
答案： 解：有两种情况：
(1)当小猫 C 在 AO 上爬行时，设 x(0＜x≤50)s 后，以这两只小猫所在位置与点 O 为顶点的三角形的面积为$1800\ cm^{2}$，由题意，得$\frac{1}{2}×3x×(100-2x)=1800$，整理，得$x^{2}-50x+600=0$，解得$x_{1}=20$，$x_{2}=30$。
(2)当小猫 C 在 OB 上爬行时，设 y(50＜y≤100)s 后，以这两只小猫所在位置与点 O 为顶点的三角形的面积为$1800\ cm^{2}$，由题意，得$\frac{1}{2}×3y×(2y-100)=1800$，整理，得$y^{2}-50y-600=0$，解得$y_{1}=60$，$y_{2}=-10$(舍去)。
答：20 s 或 30 s 或 60 s 后，以这两只小猫所在位置与点 O 为顶点的三角形的面积是$1800\ cm^{2}$。

2. 龙华天虹商场以 $ 120 $ 元/件的价格购进一批上衣，以 $ 200 $ 元/件的价格出售，每周可售出 $ 100 $ 件.为了促销，该商场决定降价销售，尽快减少库存.经调查发现，这种上衣每降价 $ 5 $ 元/件，每周可多售出 $ 20 $ 件.另外，每周的房租等固定成本共 $ 3000 $ 元.该商场要想每周盈利 $ 8000 $ 元，应将每件上衣的售价降低多少元?

答案： 解：设每件上衣的售价降低 x 元，则每件上衣的利润为(80-x)元，由题意得$(80-x)\left(100+\frac{20}{5}x\right)-3000=8000$，解得$x_{1}=30$，$x_{2}=25$。因为要尽快减少库存，所以 x=30。
答：应将每件上衣的售价降低 30 元。