《2025年新课标同步单元练习九年级数学上册北师大版深圳专版》

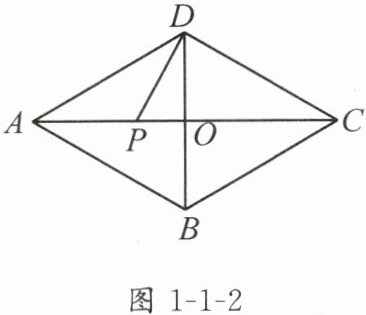
7. 如图 1 - 1 - 2，已知在菱形 $ABCD$ 中，对角线 $AC$，$BD$ 相交于点 $O$，$\angle DAB = 60^{\circ}$，$AB = 4$，点 $P$ 是线段 $AO$ 上一点，$PD=\sqrt{5}$，求 $AP$ 的长.

答案： 解：因为四边形ABCD是菱形，
所以$AB=AD$，$DB \perp AC$，$DO=\frac{1}{2}DB$.
因为$\angle DAB=60°$，
所以$\triangle ADB$是等边三角形，
所以$DO=\frac{1}{2}DB=\frac{1}{2}AB=2$.
在$Rt\triangle ADO$中，
$AO=\sqrt{AD^2-DO^2}=2\sqrt{3}$；
在$Rt\triangle DPO$中，
$PO=\sqrt{DP^2-DO^2}=1$，
所以$AP=AO-PO=2\sqrt{3}-1$.

1. 如图 1 - 1 - 3，菱形 $ABCD$ 的周长为 $40$，对角线 $AC = 12$. $E$ 是 $AD$ 上一点，过点 $E$ 作 $EG\perp AC$ 交 $AB$ 于点 $F$，交 $CB$ 的延长线于点 $G$，则 $EG$ 的长为16.

答案： 16

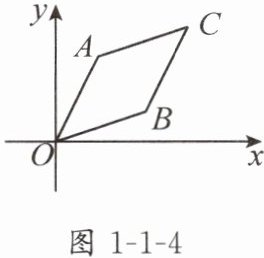
2. 如图 1 - 1 - 4，在平面直角坐标系中，已知菱形 $OACB$ 的顶点 $A$ 的坐标为 $(1,2)$，$\angle AOB = 45^{\circ}$，则点 $C$ 的坐标是$\left( \frac{3\sqrt{2}+2}{2},\frac{\sqrt{2}+4}{2} \right)$.

答案： $\left( \frac{3\sqrt{2}+2}{2},\frac{\sqrt{2}+4}{2} \right)$

3. 如图 1 - 1 - 5①，某学校的校门是伸缩门，伸缩门中每一行的菱形有 $20$ 个，每个菱形的边长为 $30\ cm$. 校门关闭时，菱形的钝角度数为 $120^{\circ}$（如图 1 - 1 - 5②）；校门部分打开时，每个菱形中的原 $120^{\circ}$ 的角缩小为 $60^{\circ}$（如图 1 - 1 - 5③）.求此时校门打开了多少米.

答案：
解：因为校门关闭时，每个菱形的钝角度数为$120°$，如答图1-1-2①，连接BD，AC相交于O，
　　　　
所以$BD=2OB=\sqrt{3}AB=30\sqrt{3}\ cm$，
所以校门关闭时，伸缩门的宽度为$600\sqrt{3}\ cm$.
因为校门部分打开时，每个菱形中的原$120°$的角缩小为$60°$，如答图1-1-2②，连接$B'D'$，
所以$B'D'=A'B'=30\ cm$，
所以校门部分打开时，伸缩门的宽度为$600\ cm$，
所以校门打开了$600\sqrt{3}-600=600(\sqrt{3}-1)(cm)=6\sqrt{3}-6(m)$.
答：此时校门打开了$(6\sqrt{3}-6)m$.