《2025年全品学练考九年级数学上册人教版江西专版》

1. 下列圆的内接正多边形中,一条边所对的圆心角最大的是(A)
A.正三角形
B.正方形
C.正五边形
D.正六边形

答案： A

2. (2024 甘孜州)如图 24-3-1,正六边形 $ ABCDEF $ 内接于 $ \odot O $,$ OA = 1 $,则 $ AB $ 的长为(C)

A.2

B.$ \sqrt{3} $
C.1
D.$ \frac{1}{2} $
]

答案： C

3. 如图 24-3-2,$ \odot O $ 是 $ \triangle ABC $ 的外接圆. 若 $ \angle ABC = 15^{\circ} $,弦 $ AC $ 是 $ \odot O $ 的内接正多边形的一边,则该正多边形是(B)

A.正二十四边形
B.正十二边形
C.正八边形
D.正六边形

答案： B

4. 我们可以只用圆规将圆等分,例如：将圆六等分,如图 24-3-3,只需在 $ \odot O $ 上任取点 $ A $,从点 $ A $ 开始,以 $ \odot O $ 的半径为半径,在 $ \odot O $ 上依次截取点 $ B $,$ C $,$ D $,$ E $,$ F $,从而点 $ A $,$ B $,$ C $,$ D $,$ E $,$ F $ 把 $ \odot O $ 六等分. 下列可以只用圆规将圆等分的是(D)
①两等分； ②三等分； ③四等分.

A.②
B.①②
C.①③
D.①②③

答案： D

5. 如图 24-3-4,要拧开一个边长是 $ 2 \, cm $ 的六角形螺帽,扳手张开的开口 $ a $ 至少应是(A)

A.$ 2\sqrt{3} \, cm $
B.$ \sqrt{3} \, cm $
C.$ \frac{2\sqrt{3}}{3} \, cm $
D.$ 1 \, cm $

答案： A

6. (2024 镇江)如图 24-3-5,$ AB $ 是 $ \odot O $ 的内接正 $ n $ 边形的一边,点 $ C $ 在 $ \odot O $ 上,$ \angle ACB = 18^{\circ} $,则 $ n = $10.
]

答案： 10

7. 如图 24-3-6,在正五边形 $ ABCDE $ 中,点 $ P $ 在 $ AD $ 上,且满足 $ PA = PE $,$ PD = AB $,则 $ \angle AEP $ 的度数是______.

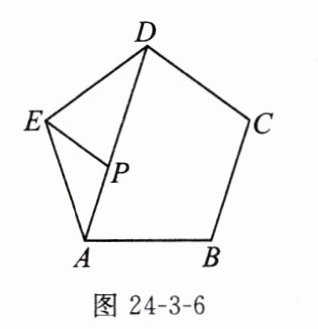
36°

答案： 36°

8. (2024 德阳改编)已知正六边形 $ ABCDEF $ 的面积为 $ 6\sqrt{3} $,则该正六边形的边长为2.

答案： 2

9. 如图 24-3-7,将正方形的四个顶点处各剪去一个直角三角形后得到一个正八边形.
(1)若正八边形的边长为 $ 2 $,则剪去的四个直角三角形的面积和为4；
(2)若原正方形的边长为 $ 2 $,求得到的正八边形的边长.
$2\sqrt{2}-2$

答案：
(1)4　
(2)$2\sqrt{2}-2$