第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
7. 如果一元二次方程 $(x - 1)^{2} = x - 1$ 的两个根分别是等腰三角形的两条边长,那么这个等腰三角形的周长为
5
.
答案:
5
8. “降次”是解一元二次方程的基本思想,用这种思想解高次方程 $x^{3} - 4x = 0$,则它的解是
x₁=0,x₂=-2,x₃=2
.
答案:
x₁=0,x₂=-2,x₃=2
9. (教材练习 T2 变式)如图 21 - 2 - 3,把小圆形场地的半径增加 $6m$ 得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为
]

(6+6$\sqrt{2}$)
m.]

答案:
(6+6$\sqrt{2}$)
10. 已知 $m,n$ 为实数,且 $(m^{2} + n^{2})(m^{2} + n^{2} - 2) = 15$,求 $m^{2} + n^{2}$ 的值.
答案:
5
1. (1)将 $2x^{2} - 3x - 2$ 进行因式分解,我们可以按下面的方法解答:
解:①竖分二次项与常数项:$2x^{2} = x\cdot 2x,-2 = (-2)×1$.
②交叉相乘,验中项(交叉相乘后的结果相加,其结果须等于多项式中的一次项):
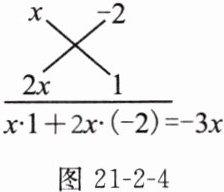
③横向写出两因式:$2x^{2} - 3x - 2 = (x - 2)(2x + 1)$.
我们把这种用十字交叉相乘分解因式的方法叫十字相乘法.
(2)根据乘法原理:若 $ab = 0$,则 $a = 0$,或 $b = 0$.
试用上述方法和原理解下列方程:
① $x^{2} - 3x + 2 = 0$;
② $x^{2} - x - 6 = 0$;
③ $x^{2} - (\sqrt{2} + \sqrt{3})x + \sqrt{6} = 0$;
④ $2x^{2} + x - 6 = 0$.
解:①竖分二次项与常数项:$2x^{2} = x\cdot 2x,-2 = (-2)×1$.
②交叉相乘,验中项(交叉相乘后的结果相加,其结果须等于多项式中的一次项):
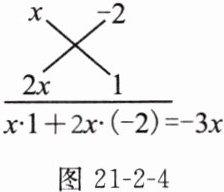
③横向写出两因式:$2x^{2} - 3x - 2 = (x - 2)(2x + 1)$.
我们把这种用十字交叉相乘分解因式的方法叫十字相乘法.
(2)根据乘法原理:若 $ab = 0$,则 $a = 0$,或 $b = 0$.
试用上述方法和原理解下列方程:
① $x^{2} - 3x + 2 = 0$;
② $x^{2} - x - 6 = 0$;
③ $x^{2} - (\sqrt{2} + \sqrt{3})x + \sqrt{6} = 0$;
④ $2x^{2} + x - 6 = 0$.
①$x₁=1,x₂=2$ ②$x₁=3,x₂=-2$ ③$x₁=\sqrt{3},x₂=\sqrt{2}$ ④$x₁=\frac{3}{2},x₂=-2$
答案:
①x₁=1,x₂=2 ②x₁=3,x₂=-2 ③x₁=$\sqrt{3}$,x₂=$\sqrt{2}$ ④x₁=$\frac{3}{2}$,x₂=-2
2. 方程 $x^{2} + x - 12 = 0$ 的解是
x₁=-4,x₂=3
.
答案:
x₁=-4,x₂=3
3. 已知 $x^{2} + xy - 6y^{2} = 0(xeq0$ 且 $yeq0)$,则 $\frac{y}{x}$ 的值是
-$\frac{1}{3}$或$\frac{1}{2}$
.
答案:
-$\frac{1}{3}$或$\frac{1}{2}$
查看更多完整答案,请扫码查看


