《2025年全品学练考九年级数学上册人教版江西专版》

12. (2024 南充)已知 $x_{1},x_{2}$是关于 $x$ 的方程 $x^{2}-2kx + k^{2}-k + 1 = 0$的两个不等的实数根。
(1)求 $k$ 的取值范围；
(2)若 $k ＜ 5$,且 $k,x_{1},x_{2}$都是整数,求 $k$ 的值。

答案：
(1)$k＞1$
(2)2

13. (2024 辽宁)某商场出售一种商品,经市场调查发现,日销售量 $y$(件)与每件售价 $x$(元)之间满足一次函数关系,部分数据如下表所示：

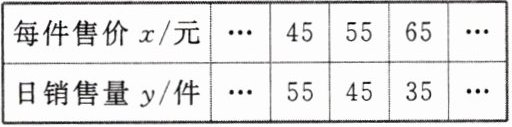
(1)求 $y$ 与 $x$ 之间的函数解析式(不要求写出自变量 $x$ 的取值范围)。
(2)该商品日销售额能否达到 2600 元？如果能,求出每件售价；如果不能,说明理由。

答案：
(1)$y=-x+100$
(2)不能.理由如下:假设该商品日销售额能达到2600元,则$x(-x+100)=2600$,整理,得$x^{2}-100x+2600=0$.$\because\Delta=(-100)^{2}-4×1×2600=-400＜0$,$\therefore$方程没有实数根,故该商品日销售额不能达到2600元.

14. (2024 淄博)“我运动,我健康,我快乐！”随着人们对身心健康的关注度越来越高,某市参加健身运动的人数逐年增多,从 2021 年的 32 万人增加到 2023 年的 50 万人。
(1)求该市参加健身运动人数的年平均增长率。
(2)为支持市民的健身运动,市政府决定从 A 公司购买某种套装健身器材。该公司规定：若购买不超过 100 套,每套售价 1600 元；若超过 100 套,每增加 10 套,每套售价可降低 40 元,但最低售价不得少于 1000 元。已知市政府向该公司支付货款 24 万元,求购买的这种健身器材的套数。

答案：
(1)25%
(2)200套