第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
10. 已知等腰三角形 $ABC$ 的底边长为 $5$,其腰长恰好是一元二次方程 $x^{2} - 2(m + 1)x + 6m - 2 = 0$ 的两个相等的实数根,则 $m$ 的值是(
A.$2$
B.$4$
C.$1$
D.$3$
D
)A.$2$
B.$4$
C.$1$
D.$3$
答案:
D
11. 用公式法解下列方程:
(1) $6x^{2} - 11x + 4 = 2x - 2$;
(2) $3x(x - 3) = 2(x - 1)(x + 1)$.
(1) $6x^{2} - 11x + 4 = 2x - 2$;
(2) $3x(x - 3) = 2(x - 1)(x + 1)$.
答案:
(1)$x_{1}=\frac {3}{2}$,$x_{2}=\frac {2}{3}$
(2)$x_{1}=\frac {9+\sqrt {73}}{2}$,$x_{2}=\frac {9-\sqrt {73}}{2}$
(1)$x_{1}=\frac {3}{2}$,$x_{2}=\frac {2}{3}$
(2)$x_{1}=\frac {9+\sqrt {73}}{2}$,$x_{2}=\frac {9-\sqrt {73}}{2}$
12. 已知关于 $x$ 的一元二次方程 $ax^{2} + bx + 1 = 0$.
(1) 当 $b = a + 2$ 时,判断方程根的情况;
(2) 若方程有两个相等的实数根,写出一组满足条件的 $a$,$b$ 的值,并求此时方程的根.
(1) 当 $b = a + 2$ 时,判断方程根的情况;
(2) 若方程有两个相等的实数根,写出一组满足条件的 $a$,$b$ 的值,并求此时方程的根.
答案:
(1)方程有两个不等的实数根
(2)可取b=2,a=1,则原方程变为$x^{2}+2x-$1=0,解得$x_{1}=x_{2}=-1$(本题答案不唯一)
(1)方程有两个不等的实数根
(2)可取b=2,a=1,则原方程变为$x^{2}+2x-$1=0,解得$x_{1}=x_{2}=-1$(本题答案不唯一)
13. 核心素养 创新意识 古希腊数学家丢番图在《算术》中就提到了一元二次方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解.在欧几里得的《几何原本》中,形如 $x^{2} + ax = b^{2}(a > 0,b > 0)$ 的方程的图解法是:如图 21-2-2,以 $\frac{a}{2}$ 和 $b$ 为两直角边长作 $Rt\triangle ABC$,再在斜边上截取 $BD = \frac{a}{2}$,则 $AD$ 的长就是所求方程的根.
(1) 请用含字母 $a$,$b$ 的式子表示 $AD$ 的长;
(2) 请利用公式法说明该图解法的正确性,并说说这种解法的遗憾之处.
]
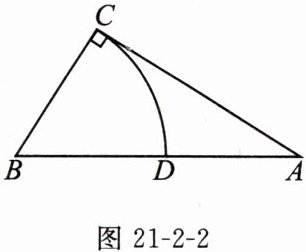
(1) 请用含字母 $a$,$b$ 的式子表示 $AD$ 的长;
(2) 请利用公式法说明该图解法的正确性,并说说这种解法的遗憾之处.
]

答案:
解:
(1)由题意可知$∠ACB=90^{\circ }$,$BC=\frac {a}{2}$,$AC=b$,
$\therefore AB=\sqrt {b^{2}+\frac {a^{2}}{4}}$,
$\therefore AD=AB-BD=\sqrt {b^{2}+\frac {a^{2}}{4}}-\frac {a}{2}=\frac {-a+\sqrt {4b^{2}+a^{2}}}{2}$.
(2)用求根公式求得$x_{1}=\frac {-a+\sqrt {4b^{2}+a^{2}}}{2}$,$x_{2}=\frac {-a-\sqrt {4b^{2}+a^{2}}}{2}$,
$\therefore AD$的长就是方程的正根.
遗憾之处:图解法不能表示方程的负根.
(1)由题意可知$∠ACB=90^{\circ }$,$BC=\frac {a}{2}$,$AC=b$,
$\therefore AB=\sqrt {b^{2}+\frac {a^{2}}{4}}$,
$\therefore AD=AB-BD=\sqrt {b^{2}+\frac {a^{2}}{4}}-\frac {a}{2}=\frac {-a+\sqrt {4b^{2}+a^{2}}}{2}$.
(2)用求根公式求得$x_{1}=\frac {-a+\sqrt {4b^{2}+a^{2}}}{2}$,$x_{2}=\frac {-a-\sqrt {4b^{2}+a^{2}}}{2}$,
$\therefore AD$的长就是方程的正根.
遗憾之处:图解法不能表示方程的负根.
查看更多完整答案,请扫码查看


