第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
9. (2023德阳)将一副三角尺 $ DOE $ 与 $ AOC $ 叠放在一起,如图23-Y-8①, $ \angle O = 90^{\circ} $, $ \angle A = 30^{\circ} $, $ \angle E = 45^{\circ} $, $ OD > OC $.将三角尺 $ DOE $ 绕点 $ O $ 顺时针旋转 $ \alpha(0^{\circ} < \alpha < 90^{\circ}) $ 到 $ \triangle D_1OE_1 $ 的位置,使 $ OD_1 // AC $,如图②.
(1)求 $ \alpha $ 的值;
(2)如图③,继续将三角尺 $ DOE $ 绕点 $ O $ 顺时针旋转,使点 $ E $ 落在 $ AC $ 边上的点 $ E_2 $ 处,点 $ D $ 落在点 $ D_2 $ 处,设 $ E_2D_2 $ 交 $ OD_1 $ 于点 $ G $, $ OE_1 $ 交 $ AC $ 于点 $ H $,若 $ G $ 是 $ E_2D_2 $ 的中点,试判断四边形 $ OHE_2G $ 的形状,并说明理由.
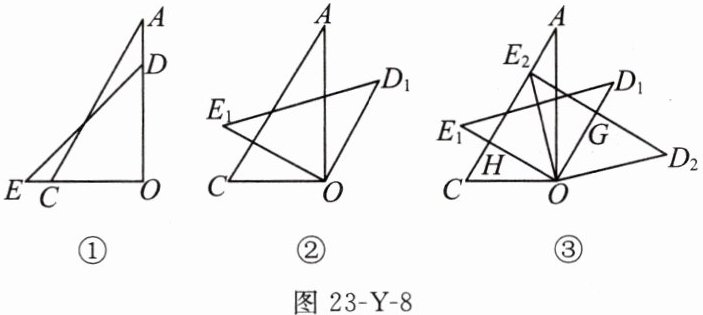
(1)求 $ \alpha $ 的值;
(2)如图③,继续将三角尺 $ DOE $ 绕点 $ O $ 顺时针旋转,使点 $ E $ 落在 $ AC $ 边上的点 $ E_2 $ 处,点 $ D $ 落在点 $ D_2 $ 处,设 $ E_2D_2 $ 交 $ OD_1 $ 于点 $ G $, $ OE_1 $ 交 $ AC $ 于点 $ H $,若 $ G $ 是 $ E_2D_2 $ 的中点,试判断四边形 $ OHE_2G $ 的形状,并说明理由.

答案:
(1)$\alpha = 30^{\circ}$
(2)四边形$OHE_{2}G$是正方形.理由如下:$\because \angle E_{2}OD_{2}=90^{\circ}$,$OD_{2}=OE_{2}$,G是$E_{2}D_{2}$的中点,$\therefore E_{2}G = OG$,$E_{2}G\perp OG$,$\therefore \angle OGE_{2}=90^{\circ}$.$\because OD_{1}// AC$,$\therefore \angle CE_{2}G=180^{\circ}-\angle OGE_{2}=90^{\circ}$.又$\because \angle HOG = 90^{\circ}$,$\therefore$四边形$OHE_{2}G$是矩形.又$\because E_{2}G = OG$,$\therefore$四边形$OHE_{2}G$是正方形.
(1)$\alpha = 30^{\circ}$
(2)四边形$OHE_{2}G$是正方形.理由如下:$\because \angle E_{2}OD_{2}=90^{\circ}$,$OD_{2}=OE_{2}$,G是$E_{2}D_{2}$的中点,$\therefore E_{2}G = OG$,$E_{2}G\perp OG$,$\therefore \angle OGE_{2}=90^{\circ}$.$\because OD_{1}// AC$,$\therefore \angle CE_{2}G=180^{\circ}-\angle OGE_{2}=90^{\circ}$.又$\because \angle HOG = 90^{\circ}$,$\therefore$四边形$OHE_{2}G$是矩形.又$\because E_{2}G = OG$,$\therefore$四边形$OHE_{2}G$是正方形.
10. (2024北京)已知 $ \angle MAN = \alpha(0^{\circ} < \alpha < 45^{\circ}) $,点 $ B $, $ C $ 分别在射线 $ AN $, $ AM $ 上,将线段 $ BC $ 绕点 $ B $ 顺时针旋转 $ 180^{\circ} - 2\alpha $ 得到线段 $ BD $,过点 $ D $ 作 $ AN $ 的垂线交射线 $ AM $ 于点 $ E $.
(1)如图23-Y-9①,当点 $ D $ 在射线 $ AN $ 上时,求证: $ C $ 是 $ AE $ 的中点;
(2)如图②,当点 $ D $ 在 $ \angle MAN $ 内部时,作 $ DF // AN $,交射线 $ AM $ 于点 $ F $,用等式表示线段 $ EF $ 与 $ AC $ 的数量关系,并证明.

(1)如图23-Y-9①,当点 $ D $ 在射线 $ AN $ 上时,求证: $ C $ 是 $ AE $ 的中点;
(2)如图②,当点 $ D $ 在 $ \angle MAN $ 内部时,作 $ DF // AN $,交射线 $ AM $ 于点 $ F $,用等式表示线段 $ EF $ 与 $ AC $ 的数量关系,并证明.

答案:
解:
(1)证明:如图①,连接CD. 由题意,得$BC = BD$,$\angle CBD = 180^{\circ}-2\alpha$,$\therefore \angle BDC=\angle BCD=\frac{1}{2}(180^{\circ}-\angle CBD)=\alpha$,$\therefore \angle BDC = \angle A$,$\therefore CA = CD$.$\because DE\perp AN$,$\therefore \angle 1+\angle A=\angle 2+\angle BDC = 90^{\circ}$,$\therefore \angle 1 = \angle 2$,$\therefore CD = CE$,$\therefore CA = CE$,$\therefore$ C是AE的中点.
由题意,得$BC = BD$,$\angle CBD = 180^{\circ}-2\alpha$,$\therefore \angle BDC=\angle BCD=\frac{1}{2}(180^{\circ}-\angle CBD)=\alpha$,$\therefore \angle BDC = \angle A$,$\therefore CA = CD$.$\because DE\perp AN$,$\therefore \angle 1+\angle A=\angle 2+\angle BDC = 90^{\circ}$,$\therefore \angle 1 = \angle 2$,$\therefore CD = CE$,$\therefore CA = CE$,$\therefore$ C是AE的中点.
(2)$EF = 2AC$.证明如下:如图②,在射线AM上取一点H,使得$BH = BA$,取EF的中点G,连接DH,DG. $\because BH = BA$,$\therefore \angle BAH=\angle BHA=\alpha$,$\therefore \angle ABH = 180^{\circ}-2\alpha=\angle CBD$,$\therefore \angle ABC = \angle HBD$.又$\because BC = BD$,$\therefore \triangle ABC\cong\triangle HBD(SAS)$,$\therefore AC = HD$,$\angle BHD = \angle A=\alpha$,$\therefore \angle FHD=\angle BHA+\angle BHD = 2\alpha$.$\because DF// AN$,$\therefore \angle EFD = \angle A=\alpha$,$\angle EDF=\angle 3 = 90^{\circ}$.$\because$ G是EF的中点,$\therefore GF = GD$,$EF = 2GD$,$\therefore \angle GFD=\angle GDF=\alpha$,$\therefore \angle HGD = 2\alpha$,$\therefore \angle HGD=\angle FHD$,$\therefore GD = HD$.$\because AC = HD$,$\therefore GD = AC$,$\therefore EF = 2AC$
$\because BH = BA$,$\therefore \angle BAH=\angle BHA=\alpha$,$\therefore \angle ABH = 180^{\circ}-2\alpha=\angle CBD$,$\therefore \angle ABC = \angle HBD$.又$\because BC = BD$,$\therefore \triangle ABC\cong\triangle HBD(SAS)$,$\therefore AC = HD$,$\angle BHD = \angle A=\alpha$,$\therefore \angle FHD=\angle BHA+\angle BHD = 2\alpha$.$\because DF// AN$,$\therefore \angle EFD = \angle A=\alpha$,$\angle EDF=\angle 3 = 90^{\circ}$.$\because$ G是EF的中点,$\therefore GF = GD$,$EF = 2GD$,$\therefore \angle GFD=\angle GDF=\alpha$,$\therefore \angle HGD = 2\alpha$,$\therefore \angle HGD=\angle FHD$,$\therefore GD = HD$.$\because AC = HD$,$\therefore GD = AC$,$\therefore EF = 2AC$
解:
(1)证明:如图①,连接CD.
 由题意,得$BC = BD$,$\angle CBD = 180^{\circ}-2\alpha$,$\therefore \angle BDC=\angle BCD=\frac{1}{2}(180^{\circ}-\angle CBD)=\alpha$,$\therefore \angle BDC = \angle A$,$\therefore CA = CD$.$\because DE\perp AN$,$\therefore \angle 1+\angle A=\angle 2+\angle BDC = 90^{\circ}$,$\therefore \angle 1 = \angle 2$,$\therefore CD = CE$,$\therefore CA = CE$,$\therefore$ C是AE的中点.
由题意,得$BC = BD$,$\angle CBD = 180^{\circ}-2\alpha$,$\therefore \angle BDC=\angle BCD=\frac{1}{2}(180^{\circ}-\angle CBD)=\alpha$,$\therefore \angle BDC = \angle A$,$\therefore CA = CD$.$\because DE\perp AN$,$\therefore \angle 1+\angle A=\angle 2+\angle BDC = 90^{\circ}$,$\therefore \angle 1 = \angle 2$,$\therefore CD = CE$,$\therefore CA = CE$,$\therefore$ C是AE的中点.(2)$EF = 2AC$.证明如下:如图②,在射线AM上取一点H,使得$BH = BA$,取EF的中点G,连接DH,DG.
 $\because BH = BA$,$\therefore \angle BAH=\angle BHA=\alpha$,$\therefore \angle ABH = 180^{\circ}-2\alpha=\angle CBD$,$\therefore \angle ABC = \angle HBD$.又$\because BC = BD$,$\therefore \triangle ABC\cong\triangle HBD(SAS)$,$\therefore AC = HD$,$\angle BHD = \angle A=\alpha$,$\therefore \angle FHD=\angle BHA+\angle BHD = 2\alpha$.$\because DF// AN$,$\therefore \angle EFD = \angle A=\alpha$,$\angle EDF=\angle 3 = 90^{\circ}$.$\because$ G是EF的中点,$\therefore GF = GD$,$EF = 2GD$,$\therefore \angle GFD=\angle GDF=\alpha$,$\therefore \angle HGD = 2\alpha$,$\therefore \angle HGD=\angle FHD$,$\therefore GD = HD$.$\because AC = HD$,$\therefore GD = AC$,$\therefore EF = 2AC$
$\because BH = BA$,$\therefore \angle BAH=\angle BHA=\alpha$,$\therefore \angle ABH = 180^{\circ}-2\alpha=\angle CBD$,$\therefore \angle ABC = \angle HBD$.又$\because BC = BD$,$\therefore \triangle ABC\cong\triangle HBD(SAS)$,$\therefore AC = HD$,$\angle BHD = \angle A=\alpha$,$\therefore \angle FHD=\angle BHA+\angle BHD = 2\alpha$.$\because DF// AN$,$\therefore \angle EFD = \angle A=\alpha$,$\angle EDF=\angle 3 = 90^{\circ}$.$\because$ G是EF的中点,$\therefore GF = GD$,$EF = 2GD$,$\therefore \angle GFD=\angle GDF=\alpha$,$\therefore \angle HGD = 2\alpha$,$\therefore \angle HGD=\angle FHD$,$\therefore GD = HD$.$\because AC = HD$,$\therefore GD = AC$,$\therefore EF = 2AC$ 查看更多完整答案,请扫码查看


