《2025年全品学练考九年级数学上册人教版江西专版》

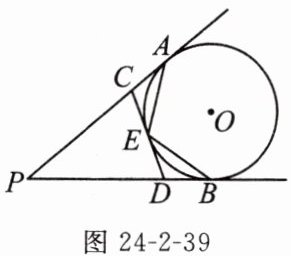
10. 如图 24-2-39,PA,PB,CD 分别与⊙O 相切于点 A,B,E,CD 与 PA,PB 分别相交于 C,D 两点. 若∠P = 40°,则∠PAE + ∠PBE 的度数为 (D)

A.50°
B.62°
C.66°
D.70°

答案： D

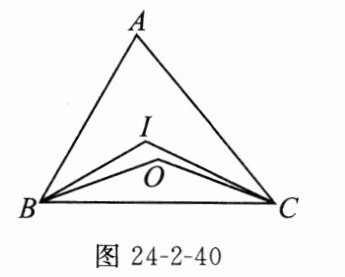
11. 如图 24-2-40,点 O 为△ABC 的外心,点 I 为△ABC 的内心. 若∠BOC = 140°,则∠BIC 的度数为125°.

答案： 125°

12. 如图 24-2-41,在△ABC 中,∠ABC = 90°,在 AB 上取一点 E,以 BE 为直径的⊙O 与 AC 相切于点 D,AE = 2 cm,AD = 4 cm.
(1)⊙O 的直径 BE 为6cm；
(2)求△ABC 的面积.
24cm²

答案：
(1)6
(2)24cm²

13. (2024 陕西)问题提出
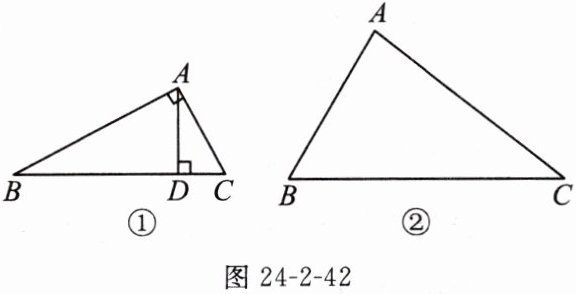
(1)如图 24-2-42①,在△ABC 中,∠BAC = 90°,AD⊥BC,垂足为 D. 若 AB = 15,AC = 8,则 AD 的长为______.
问题解决
(2)如图②所示,某工厂剩余一块三角形板材 ABC,其中 AB = 100 cm,BC = 160 cm,AC = 140 cm. 为了充分利用材料,工人师傅想用这块板材裁出一个尽可能大的圆形部件. 你认为可以吗？若可以,请在图中确定可裁出的最大圆形部件的圆心 O 的位置,并求出⊙O 的半径；若不可以,请说明理由.

答案：
解:
(1)$\frac{120}{17}$
(2)可以.
∵三角形内最大的圆是三角形的内切圆，
∴所求圆的圆心是△ABC的内心.
如图，作∠ABC和∠ACB的平分线BE，CF交于点O，则点O就是裁出的最大圆形部件的圆心O的位置.
过点O作OH⊥BC于点H，OP⊥AC于点P，OQ⊥AB于点Q，连接OA，OB，OC，过点A作AM⊥BC于点M.

设BM=x cm，$\odot O$的半径为R cm.
∵BC=160 cm，
∴CM=(160 - x)cm.
在Rt△ABM中，由勾股定理，得$AM^{2}=AB^{2}-BM^{2}=100^{2}-x^{2}$.
在Rt△ACM中，由勾股定理，得$AM^{2}=AC^{2}-CM^{2}=140^{2}-(160 - x)^{2}$，
∴$100^{2}-x^{2}=140^{2}-(160 - x)^{2}$，
解得x=50，
∴$AM=\sqrt{100^{2}-x^{2}}=50\sqrt{3}(cm)$，
∴$S_{\triangle ABC}=\frac{1}{2}BC\cdot AM=\frac{1}{2}×160×50\sqrt{3}=4000\sqrt{3}(cm^{2})$.
∵点O为△ABC的内心，
∴OH=OP=OQ=R cm.
∵$S_{\triangle OBC}+S_{\triangle OCA}+S_{\triangle OAB}=S_{\triangle ABC}$，
∴$\frac{1}{2}BC\cdot OH+\frac{1}{2}AC\cdot OP+\frac{1}{2}AB\cdot OQ=4000\sqrt{3}$，
即$(160 + 140 + 100)R=8000\sqrt{3}$，
∴$R=20\sqrt{3}$，
即$\odot O$的半径为$20\sqrt{3}$ cm.