《2025年同步导学与优化训练七年级数学上册人教版》

1. 若 $a^{2}+|b + 1| = 0$,则 $(a + b)^{2025}$ 的值为(A)
A.$-1$
B.$0$
C.$1$
D.$2$

答案： 1.A 解析:由题意,得a=0,b+1=0.所以a=0,b=-1.所以$(a+b)^{2025}=(0-1)^{2025}=(-1)^{2025}=-1.$故选A.

2. 若 $m^{2}+2m - 1 = 0$,则 $2m^{2}+4m - 3$ 的值是(A)
A.$-1$
B.$-5$
C.$5$
D.$-3$

答案： 2.A 解析$:2m^{2}+4m-3=2(m^{2}+2m-1)-1=0-1=-1.$故选A.

3. 若 $a$,$b$ 非零且互为相反数,$c$,$d$ 互为倒数,$m$ 的绝对值为 $2$,则 $m^{2}-cd+\frac{a + b}{m}$ 的值为(3)
A.$-4$
B.$0$
C.$3$
D.$5$

答案： 3.C 解析:因为a,b非零且互为相反数,所以a+b=0.因为c,d互为倒数,所以cd=1.因为m的绝对值为2,所以$m^{2}=4.$所以$m^{2}-cd+\frac{a+b}{m}=4-1+0=3.$

4. (跨学科融合)已知摄氏温度 $(^{\circ}C)$ 与华氏温度 $(^{\circ}F)$ 之间的转换关系为 $t_{C}= \frac{5}{9}(t_{F}-32)$ 或 $t_{F}= 32+\frac{9}{5}t_{C}$($t_{C}$ 表示摄氏温度,$t_{F}$ 表示华氏温度)。某天纽约的最高气温是 $64.4^{\circ}F$,上海的最高气温是 $18^{\circ}C$,则这一天纽约的最高气温等于上海的最高气温。(填“高于”“低于”或“等于”)

答案： 4.等于 解析:因为纽约的最高气温是64.4°F,所以其摄氏温度为$\frac{5}{9}×(64.4-32)=18(℃),$则这一天纽约的最高气温等于上海的最高气温.

5. 某市有一块长为 $4m$,宽为 $b m$ 的长方形地块,如图所示(单位：$m$)。规划部门计划将阴影部分绿化,中间正方形空地将修建一座雕像。用含 $a$,$b$ 的式子表示绿化的面积是$(4b-a^{2})$$m^{2}$,若 $a = 2$,$b = 3$,则绿化面积是$8$$m^{2}$。

答案： $5.(4b-a^{2}) 8 $解析:根据题意,得阴影部分的面积为$(4b-a^{2})m^{2},$即绿化的面积是$(4b-a^{2})m^{2}.$将a=2,b=3代入,得$4×3-2^{2}=8(m^{2}).$所以当a=2,b=3时,绿化面积为$8m^{2}.$

6. 甲、乙两景点是某平台国庆期间热门景点前两名,已知甲景点门票每张 $100$ 元,乙景点门票每张 $45$ 元,在某个时间段内,共售出 $a$ 张甲景点门票和 $b$ 张乙景点门票。
(1)在该时间段内,该平台这两种门票共售出多少元？
(2)当 $a = 30000$,$b = 8000$ 时,该平台这两种门票共售出多少元？(用科学记数法表示)

答案： 6.解:
(1)(100a+45b)元.
(2)当a=30000,b=8000时$,100a+45b=100×30000+45×8000=3360000=3.36×10^{6}($元).

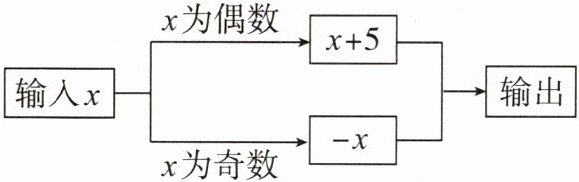
7. 如图所示,按程序计算,若输入 $x$ 的值为 $3$,则输出的值为-3。

答案： 7.-3 解析:因为3为奇数,所以将x=3代入-x,输出的值为-3.

8. 如图,两摞规格相同的数学课本整齐地叠放在课桌上,请根据示意图中的数据信息,解答下列问题：
(1)每本数学课本的高度为0.5$cm$,课桌的高度为85$cm$；
(2)当数学课本为 $x$ 本时,同样叠放在桌面上的一摞数学课本高出地面的距离为(0.5x+85)$cm$(用含 $x$ 的代数式表示)；
(3)桌面上有 $55$ 本数学课本,整齐叠放成一摞,若有 $18$ 名同学各从中取走 $1$ 本,求余下的数学课本高出地面的距离。
解：共有55本数学课本，18名同学各取走1本后，剩余课本数量为55-18=37本。根据（2）中代数式，余下的数学课本高出地面的距离为0.5×37+85=18.5+85=103.5cm。

答案： 8.解:
(1)88-86.5=1.5(cm)是3本数学课本的高度,所以1.5÷3=0.5(cm)是每本数学课本的高度,所以86.5-0.5×3=85(cm)是课桌的高度.故答案为0.5;85.
(2)桌面上有x本数学课本,每本数学课本的高度是0.5cm,所以x本数学课本的高度是0.5x cm,所以高出地面的距离是(0.5x+85)cm.故答案为(0.5x+85).
(3)共有55本数学课本,有18名同学各取走1本,所以桌面上还有55-18=37(本)数学课本.所以余下的数学课本高出地面的距离是0.5x+85=0.5×37+85=18.5+85=103.5(cm).