《2025年同步导学与优化训练七年级数学上册人教版》

1. 数轴上表示$-3$的点在原点的左侧,距离原点(3个单位长度)
A.0 个单位长度
B.1 个单位长度
C.2 个单位长度
D.3 个单位长度

答案： D解析:数轴上表示−3的点在原点的左侧，距离原点3个单位长度.故选D.

2. 如图,数轴上标出的点$A$表示的数为(C)

A.30
B.50
C.60
D.80

答案： C　解析:每个小间隔表示的长度为100÷5=20，点A离原点3个小间隔，因此点A 表示的数为20×3=60.

3. 数轴上$A$,$B两点表示的有理数分别是-3\frac{1}{2}$和 2,则$A$,$B$两点间的距离是$5\frac{1}{2}$.

答案： $5\frac{1}{2}　$解析:因为$2+3\frac{1}{2}=5\frac{1}{2}，$所以A,B 两点间的距离是$5\frac{1}{2}.$

4. 在正方向向右的数轴上,点$A和点B表示的数分别为-2$和 1,若要使点$A表示的数是点B$表示的数的 3 倍,应把点$A$向右移动5个单位长度.

答案： 5　解析:点A应从表示−2的点移动到表示3的点，而−2与原点相距2个单位长度，3与原点相距3个单位长度，故点A应向右移动5个单位长度.

5. 请把下面不完整的数轴画完整,并在数轴上表示下列各数：$-3$,$-\frac{1}{2}$,4.

答案：
解:如图所示.

6. 小华骑车从家出发,先向东骑行 2 km 到达 A 村,再继续向东骑行 3 km 到达 B 村,接着又向西骑行 9 km 到达 C 村,最后回到家.试解答下列问题：
(1)以家为原点,以向东方向为正方向,在下面给定的数轴上标上单位长度,并表示出家以及 A,B,C 三个村庄的位置.

(2)C 村离 A 村有多远？
(3)小华一共骑行了多少千米？

答案：
解:
(1)如图所示.(画法不唯一)

C村家A村B村−4−3−2−10123456
(2)C村离A村有2+4=6(km).
(3)小华一共骑行了2+3+9+4=18(km).

7. (新定义题)数轴上表示整数的点称为整点.某数轴的单位长度是 1 cm,若在这个数轴上随意画出一条长 2 024 cm 的线段$AB$,则线段$AB$盖住的整点个数是(D)
A.2 021 或 2 022
B.2 022 或 2 023
C.2 023 或 2 024
D.2 024 或 2 025

答案： D解析:分两种情况.①当线段AB的起点是整点时，终点也落在整点上，那就盖住了2025个整点;②当线段AB的起点不是整点时，终点也不落在整点上，那么线段AB就盖住了2024个整点.

8. 点$A$是数轴上一点,一只蚂蚁从点$A$出发向某一方向爬行 5 个单位长度到了表示数 2 的点,则点$A$所表示的数是−3或7.

答案： −3或7　解析:依题意，得若点A在表示数2的点的左侧，则点A所表示的数是−3;若点A在表示数2的点的右侧，则点A所表示的数是7.因此，点A所表示的数是−3或7.

9. (综合与实践)操作探究：在一张纸上有一条数轴,如图所示.

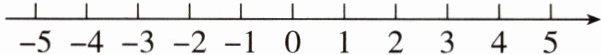
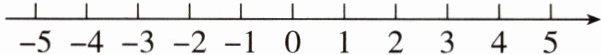
(1)折叠这张纸,使表示数 1 的点与表示数$-1$的点重合,则表示数$-3$的点与表示数3的点重合.
(2)折叠这张纸,使表示数$-1$的点与表示数 3 的点重合,回答以下问题：
①表示数 5 的点与表示数-3的点重合.
②若数轴上$A$,$B$两点的距离是 11(点$A在点B$的左侧),且$A$,$B$两点经折叠后重合,$A$,$B$两点表示的数分别是多少？
解：由题意可知，折痕经过表示数1的点，A，B两点的距离为11,则A，B两点与表示数1的点的距离都是11÷2=5.5.又因为点A 在点B的左侧，所以点A表示的数是−4.5，点B表示的数是6.5.

答案： 解:
(1)因为表示数1的点与表示数−1的点重合，所以折痕过原点，所以表示数−3的点与表示数3的点重合,故答案为3.
(2)①因为表示数−1的点与表示数3的点重合，所以折痕过表示数1的点，所以表示数5 的点与表示数−3的点重合,故答案为−3.
②由题意可知，折痕经过表示数1的点，A，B两点的距离为11,则A，B两点与表示数1的点的距离都是11÷2=5.5.又因为点A 在点B的左侧，所以点A表示的数是−4.5，点B表示的数是6.5.