《2025年同步导学与优化训练七年级数学上册人教版》

1. 若数轴上表示$-1和3的两点分别是点A和点B$,则点$A和点B$之间的距离是(D)
A.$-4$
B.$-2$
C.$2$
D.$4$

答案： D

2. 若$\vert a + 3\vert+\vert b + 1\vert = 0$,则$a - b+\frac{1}{2}$的值为(C)
A.$-4\frac{1}{2}$
B.$-2\frac{1}{2}$
C.$-1\frac{1}{2}$
D.$1\frac{1}{2}$

答案： C 解析:由|a+3|+|b+1|=0,知a=-3,b=-1,所以a - b+$\frac{1}{2}$=-3-(-1)+$\frac{1}{2}$=-3+1+$\frac{1}{2}$=-1$\frac{1}{2}$.故选C.

3. 老李用$400元购进了8$套儿童服装,准备出售.如果每套儿童服装以$55$元的价格为标准,超出的记作正数,不足的记作负数,售价记录如下(单位：元)：$+2$,$-3$,$+2$,$+1$,$-2$,$-1$,$0$,$-3$,当他卖完这$8$套儿童服装后(C)
A.亏损了$4$元
B.亏损了$32$元
C.盈利了$36$元
D.盈利了$51$元

答案： C 解析:因为55×8=440(元),2-3+2+1-2-1+0-3=-4(元),所以收入为440-4=436(元),盈利为436-400=36(元).故选C.

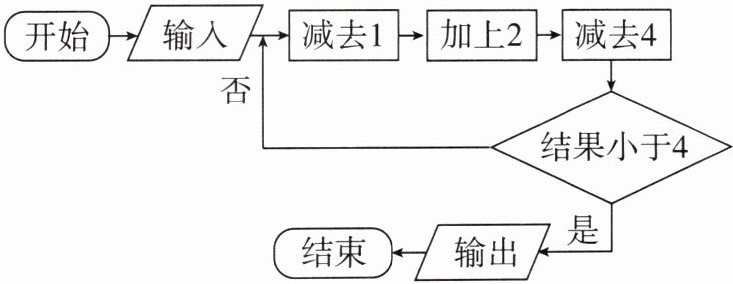
4. 如图所示,根据程序计算,若输入的值为$1$,则输出的值为-2.

答案： -2 解析:由题意知1-1+2-4=-2.因为-2＜4,所以输出的值为-2.

5. 数轴上,设点$A表示-3$,点$B表示x$,若点$A和点B的距离是6$,则$x$的值是3或-9.

答案： 3或-9 解析:由题意,得|x-(-3)|=6,所以|x+3|=6,所以x+3=6或x+3=-6,所以x=3或x=-9.

6. 计算：
(1) $-\frac{1}{2}-5\frac{1}{5}-1 + 3\frac{2}{3}-4.5 + 2\frac{1}{3}$；
(2) $(+17\frac{3}{4})-(+6.25)-(-8\frac{1}{2})-(+0.75)-22\frac{1}{4}$.

答案：
(1)原式=(-$\frac{1}{2}$-4.5)-5$\frac{1}{5}$-1+(3$\frac{2}{3}$+2$\frac{1}{3}$)=-5-5$\frac{1}{5}$-1+6=-5$\frac{1}{5}$;
(2)原式=17.75-6.25+8.5-0.75-22.25=(17.75-0.75)+(-6.25-22.25)+8.5=17-28.5+8.5=-3.

7. 如图,请根据对话解答下列问题.

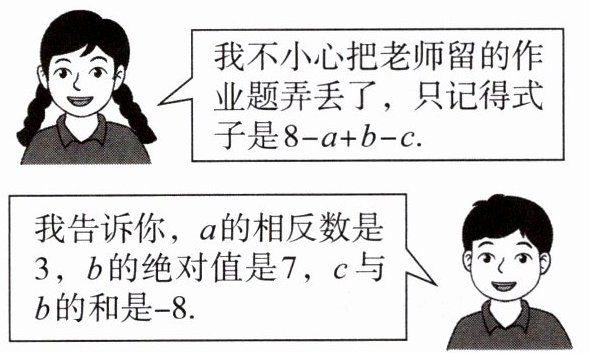
求：(1)$a$,$b$的值；
(2)$8 - a + b - c$的值.

答案：
(1)因为a的相反数是3,b的绝对值是7,所以a=-3,b=±7;
(2)因为a=-3,b=±7,c与b的和是-8,所以当b=7时,c=-15;当b=-7时,c=-1.当a=-3,b=7,c=-15时,8-a+b-c=8-(-3)+7-(-15)=33;当a=-3,b=-7,c=-1时,8-a+b-c=8-(-3)+(-7)-(-1)=5.

8. (新定义题)设$[a]表示不超过a$的最大整数,例如：$[2.3]= 2$,$[-4\frac{1}{3}]= -5$,$[5]= 5$.
(1) 求$[2\frac{1}{5}]+[-3.6]-[-7]$的值；
(2) 令$\{a\}= a - [a]$,求$\{2\frac{3}{4}\}-[-2.4]+\{-6\frac{1}{4}\}$的值.

答案：
(1)[2$\frac{1}{5}$]+[-3.6]-[-7]=2+(-4)-(-7)=2-4+7=5;
(2){2$\frac{3}{4}$}-[-2.4]+\{-6$\frac{1}{4}$}=2$\frac{3}{4}$-[2$\frac{3}{4}$-(-3)]+(-6$\frac{1}{4}$)-[-6$\frac{1}{4}$]=2$\frac{3}{4}$-2+3-$\frac{25}{4}$+7=$\frac{11}{4}$-2+3-$\frac{25}{4}$+7=8-$\frac{14}{4}$=8-3.5=4.5.