《2025年同步导学与优化训练七年级数学上册人教版》

13. 已知 $ | x | = 3 $,$ | y | = 2 $,且 $ x ＜ y $,则 $ x = $-3,$ y = $2或-2.

答案： -3 2或-2 解析:因为|x|=3,|y|=2,所以x=3或-3,y=2或-2.又因为x＜y,所以x=-3.

14. 若 $ | x - 2 | + | y + 4 | = 0 $,则 $ x = $2,$ y = $-4.

答案： 2 -4 解析:因为|x-2|+|y+4|=0,所以x-2=0,y+4=0.所以x=2,y=-4.

15. (新定义题)点 $ A $,$ B $,$ P $ 是数轴上不重合的三个点,点 $ A $ 表示的数为 $ - 3 $,点 $ B $ 表示的数为 $ 1 $,若 $ A $,$ B $,$ P $ 三个点中,其中一点到另外两点的距离相等,我们称这三个点为“和谐三点”,则符合“和谐三点”的点 $ P $ 表示的数为-7或-1或5.

答案： -7或-1或5 解析:设符合“和谐三点”的点P表示的数为x.因为点A表示的数为-3,点B表示的数为1,所以点A,B之间的距离为4.当点P在点A的左侧时,x=-7.当点P在点A,B之间时,x=-1.当点P在点B的右侧时,x=5.综上所述,符合“和谐三点”的点P表示的数为-7或-1或5.

16. 把下列各数填入它们属于的集合内:
$ 8 $,$ - 1 $,$ - 0.4 $,$ \dfrac { 3 } { 5 } $,$ 0 $,$ \dfrac { 1 } { 3 } $,$ - 1 \dfrac { 3 } { 7 } $,$ - ( - 5 ) $,$ - \left| - \dfrac { 20 } { 7 } \right| $.
正数集合:…{ };
负数集合:…{ };
整数集合:…{ };
非负有理数集合:…{ }.

答案： 解:正数集合:$\{8,\frac{3}{5},\frac{1}{3},-(-5),\cdots\}$;负数集合:$\{-1,-0.4,-1\frac{3}{7},-|-\frac{20}{7}|,\cdots\}$;整数集合:$\{8,-1,0,-(-5),\cdots\}$;非负有理数集合:$\{8,\frac{3}{5},0,\frac{1}{3},-(-5),\cdots\}$.

17. 在数轴上表示下列各数,并按从小到大的顺序用“$ ＜ $”把这些数连接起来.
$ 1.5 $,$ | + ( - 2 ) | $,$ + ( - 3 ) $,$ 0 $,$ - | - 2 | $,$ 2 \dfrac { 1 } { 2 } $.

答案：
解:$|+(-2)|=2$,$+(-3)=-3$,$-|-2|=-2$.在数轴上表示如图所示.

$+(-3)＜-|-2|＜0＜1.5＜|+(-2)|＜2\frac{1}{2}$.

18. 如图,点 $ A $ 表示的数是 $ - 4 $,点 $ D $ 表示的数是 $ - 5 $.
(1)在数轴上标出原点 $ O $;
(2)指出点 $ B $ 表示的数;
(3)若 $ C $,$ B $ 两点到原点的距离相等,且 $ C $,$ B $ 两点在原点的两侧,求点 $ C $ 表示的数.

答案：
解:
(1)如图所示.

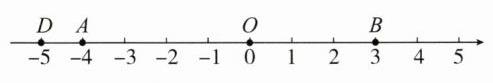
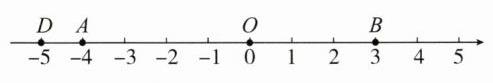
(2)点B表示的数是3.
(3)点C表示的数是-3.

19. 化简下列各数,并回答问题:
$ - ( - 2 ) $,$ + \left( - \dfrac { 1 } { 5 } \right) $,$ - [ - ( - 4 ) ] $,$ - [ - ( + 3.5 ) ] $,$ - \{ - [ - ( - 5 ) ] \} $,$ - \{ - [ - ( + 5 ) ] \} $.
(1)当 $ + 5 $ 前面有 $ 2026 $ 个负号时,化简后结果是多少?
(2)当 $ - 5 $ 前面有 $ 2025 $ 个负号时,化简后结果是多少?
(3)由(1)(2),你能总结出什么规律?

答案： 解:$-(-2)=2$.$+(-\frac{1}{5})=-\frac{1}{5}$.$-[-(-4)]=-4$.$-[-(+3.5)]=3.5$.$-\{-[-(-5)]\}=5$.$-\{-[-(+5)]\}=-5$.
(1)当+5前面有2026个负号时,化简后结果是5.
(2)当-5前面有2025个负号时,化简后结果是5.
(3)规律:一个数的前面有偶数个负号时,化简结果是这个数本身;一个数的前面有奇数个负号时,化简结果是这个数的相反数.