2025年同步导学与优化训练七年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年同步导学与优化训练七年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
22. 一则故事:在某个王国里,有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第1格放2粒米,第2格放4粒米,第3格放8粒米,然后是16粒,32粒……一直到第64格.”国王哈哈大笑.根据故事解决问题:
(1)在第64格中应放多少粒米?(用幂表示)
(2)请探究(1)中的结果的末位数字是多少.(简要写出探究过程)
(1)在第64格中应放多少粒米?(用幂表示)
(2)请探究(1)中的结果的末位数字是多少.(简要写出探究过程)
答案:
(1)因为$2 = 2^1,4 = 2^2,8 = 2^3……$所以在第64格中应放$2^64$粒米.
(2)因为$2^1=2,2^2=4,2^3=8,2^4=16,2^5=32……$所以末位数字每4个一循环,64÷4 = 16,所以$2^64$的末位数字与$2^4$的末位数字相同,是6.
(1)因为$2 = 2^1,4 = 2^2,8 = 2^3……$所以在第64格中应放$2^64$粒米.
(2)因为$2^1=2,2^2=4,2^3=8,2^4=16,2^5=32……$所以末位数字每4个一循环,64÷4 = 16,所以$2^64$的末位数字与$2^4$的末位数字相同,是6.
23. 【概念学习】
规定:求若干个相同的有理数(均不等于0)的除法的运算叫除方,如$3 ÷ 3 ÷ 3$,$(-2) ÷ (-2) ÷ (-2) ÷ (-2)$等.类比有理数的乘方,我们把3 ÷ 3 ÷ 3记作$3^③$,读作“3的圈3次方”,(-2) ÷ (-2) ÷ (-2) ÷ (-2)记作$(-2)^④$,读作“负2的圈4次方”.一般地,把 记作
记作 ,读作“$a的圈n$次方”,如
,读作“$a的圈n$次方”,如
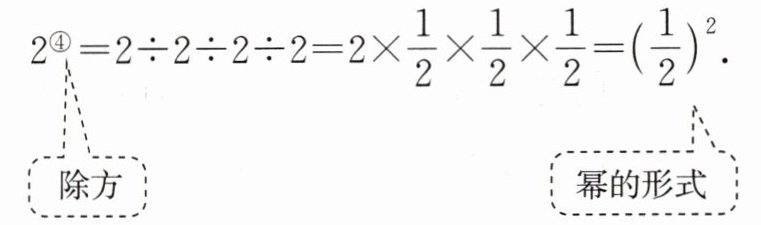
【初步探究】
(1)直接写出计算结果:$4^③$ =
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(此处不用作答)
(2)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
$(-3)^④$=
(3)想一想:将一个非零有理数$a的圈n$次方写成幂的形式是
(4)比较:$(-9)^⑤$
【灵活应用】
(5)算一算:
$12^{2} ÷ (-\frac{1}{3})^④ × (-\frac{1}{2})^⑤- (-\frac{1}{3})^⑥ + 3^{3}.$
规定:求若干个相同的有理数(均不等于0)的除法的运算叫除方,如$3 ÷ 3 ÷ 3$,$(-2) ÷ (-2) ÷ (-2) ÷ (-2)$等.类比有理数的乘方,我们把3 ÷ 3 ÷ 3记作$3^③$,读作“3的圈3次方”,(-2) ÷ (-2) ÷ (-2) ÷ (-2)记作$(-2)^④$,读作“负2的圈4次方”.一般地,把
 记作
记作 ,读作“$a的圈n$次方”,如
,读作“$a的圈n$次方”,如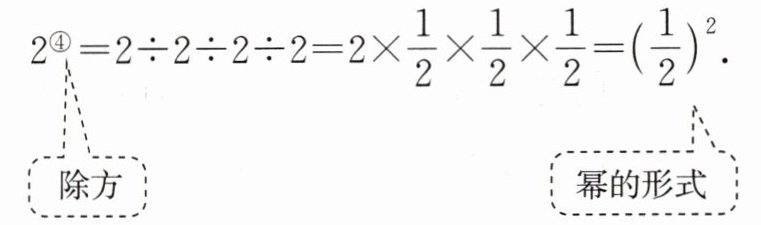
【初步探究】
(1)直接写出计算结果:$4^③$ =
$\frac{1}{4}$
,$(-\frac{1}{2})^④$= 4
.【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?(此处不用作答)
(2)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
$(-3)^④$=
$(-\frac{1}{3})^{2}$
;$5^⑥$= $(\frac{1}{5})^{4}$
;$(\frac{1}{2})^⑤ $= $2^{3}$
.(3)想一想:将一个非零有理数$a的圈n$次方写成幂的形式是
$(\frac{1}{a})^{n-2}$
.(4)比较:$(-9)^⑤$
$\gt$
$(-3)^⑦$(填“$\gt$”“$\lt$”或“$=$”).【灵活应用】
(5)算一算:
$12^{2} ÷ (-\frac{1}{3})^④ × (-\frac{1}{2})^⑤- (-\frac{1}{3})^⑥ + 3^{3}.$
原式$=144÷(-3)^{2}×(-2)^{3}-(-3)^{4}+3^{3}=144×\frac{1}{9}×(-8)-81+27=-128-81+27=-182$
答案:
(1)$\frac{1}{4}$;$4$
(2)$(-\frac{1}{3})^{2}$;$(\frac{1}{5})^{4}$;$2^{3}$
(3)$(\frac{1}{a})^{n-2}$
(4)$\gt$
(5)原式$=144÷(-3)^{2}×(-2)^{3}-(-3)^{4}+3^{3}=144×\frac{1}{9}×(-8)-81+27=-128-81+27=-182$
(1)$\frac{1}{4}$;$4$
(2)$(-\frac{1}{3})^{2}$;$(\frac{1}{5})^{4}$;$2^{3}$
(3)$(\frac{1}{a})^{n-2}$
(4)$\gt$
(5)原式$=144÷(-3)^{2}×(-2)^{3}-(-3)^{4}+3^{3}=144×\frac{1}{9}×(-8)-81+27=-128-81+27=-182$
查看更多完整答案,请扫码查看


