《2025年同步导学与优化训练七年级数学上册人教版》

14. 用简便方法计算$(-\frac{3}{2}) × (-\frac{11}{15}) - \frac{3}{2} × (-\frac{13}{15}) + \frac{3}{2} × (-\frac{14}{15})$时,常用运算律将题目变形,使运算量减小,达到简化运算的目的.请你在横线上将计算过程补充完整:原式$= (-\frac{3}{2}) × [(-\frac{11}{15}) + (-\frac{13}{15}) +$$\frac{14}{15}$$] =$1.

答案： $\frac{14}{15}$ 1 解析:$(-\frac{3}{2})\times(-\frac{11}{15})-\frac{3}{2}\times(-\frac{13}{15})+\frac{3}{2}\times(-\frac{14}{15})$$=(-\frac{3}{2})\times[(-\frac{11}{15})+(-\frac{13}{15})+\frac{14}{15}]$$=-\frac{3}{2}\times(-\frac{10}{15})$$=\frac{3}{2}\times\frac{2}{3}=1$. 

15. 小时候大家喜欢玩的幻方游戏,老师稍加修改变成了“幻圆”游戏,现在将$-1$,2,$-3$,4,$-5$,6,$-7$,8分别填入下图中的圆圈内,使横、竖直线以及内外两圈上的4个数之和都相等,老师已经帮助同学们完成了部分填空,则图中$a + b$的值为______.

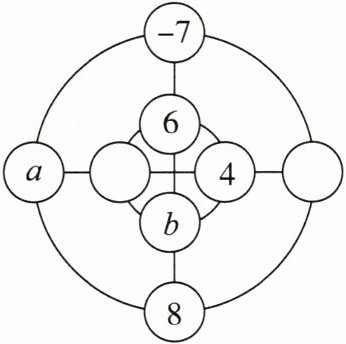
答案：
-6或-3 解析:如图,设小圈上未知的数为c,大圈上未知的数为d,-1 + 2 - 3 + 4 - 5 + 6 - 7 + 8 = 4.因为横、竖直线以及内外两圈上的4个数之和都相等,所以内外两圈上的4个数的和都是2,横、竖直线上的4个数的和也都是2. 所以b = 2 - 8 - 6 - (-7)=-5,所以c = 2 - 4 - 6 - (-5)=-3,剩下的两个数为-1和2,且满足-1 + 2 - 3 + 4 = 2,-1 + 2 - 7 + 8 = 2.当a = -1,d = 2时,a + b=-1 - 5=-6;当a = 2,d = -1时,a + b = 2 - 5=-3.

16. 简便计算:
(1)$2\frac{2}{5} + 2\frac{1}{7} + (-5\frac{1}{7}) - (-5\frac{3}{5})$;
(2)$3.75 + (-5.18) - (-2.25) + 5.18$;
(3)$(\frac{1}{4} - \frac{5}{9} - \frac{1}{3} + \frac{7}{12}) ÷ (-\frac{1}{36})$;
(4)$99\frac{17}{18} × (-9)$.

答案： 解:
(1)原式$=2\frac{2}{5}+2\frac{1}{7}-5\frac{1}{7}+5\frac{3}{5}$$=(2\frac{2}{5}+5\frac{3}{5})+(2\frac{1}{7}-5\frac{1}{7})=8-3=5$.
(2)原式$=3.75-5.18+2.25+5.18$$=(3.75+2.25)+(5.18-5.18)=6$.
(3)原式$=(\frac{1}{4}-\frac{5}{9}-\frac{1}{3}+\frac{7}{12})\times(-36)=$$\frac{1}{4}\times(-36)-\frac{5}{9}\times(-36)-\frac{1}{3}\times(-36)+\frac{7}{12}\times(-36)=-9+20+12-21=2$.
(4)原式$=(100-\frac{1}{18})\times(-9)=100\times(-9)-\frac{1}{18}\times(-9)=-900+\frac{1}{2}=-899\frac{1}{2}$. 

17. 甲、乙两名同学的身高都约是$1.6 × 10^{2}$cm,但甲却比乙高9 cm,有这种可能吗?为什么?若有,请举例说明.

答案： 解:有这种可能.当乙身高为$1.55×10^2cm,$甲身高为$1.64×10^2cm$时,他们的身高都约为$1.6×10^2cm,$但相差9 cm.