《2025年新课程自主学习与测评七年级数学上册人教版》

22. (6分)先化简,再求值：$2(x^2y+xy)-3(x^2y-xy)-4x^2y$,其中x= -1,y= 1.

答案： $-5x^{2}y+5xy$；$-10$

23. (6分)若x,y互为相反数,a,b互为倒数,c的绝对值等于2,求$(\frac{x+y}{2})^{2026}-(-ab)^{2025}+c^2$的值.

答案： 5

24. (9分)科技改变生活,当前网络销售日益盛行,许多农民采用网上销售的方式进行营销,实现了脱贫致富.小明把自家种的柚子放到网上销售,计划每天销售100kg,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负.下表是小明第一周柚子的销售情况：

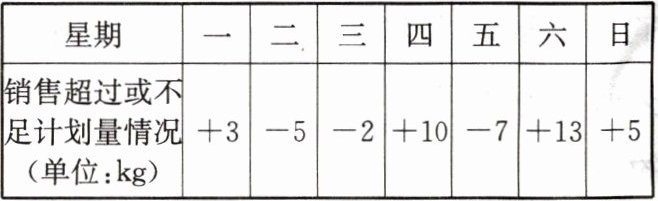
(1)小明第一周销售柚子最多的一天比最少的一天多销售多少千克？
(2)小明第一周实际销售柚子的总量是多少千克？
(3)若小明按10元/千克进行柚子销售,平均运费为3.5元/千克,则小明第一周销售柚子一共收入多少元？

答案： （1）20 kg. （2）717 kg. （3）4 660.5元

25. (8分)观察下列等式：
$2^2-2^1= 2^1$；$2^3-2^2= 2^2$；$2^4-2^3= 2^3$；……
探究其中的规律,并解答下列问题：
(1)请直接写出第4个等式：$2^{5}-2^{4}=2^{4}$；第n个等式：$2^{n+1}-2^{n}=2^{n}$.
(2)计算：$2^1-2^2-2^3-…-2^{14}+2^{15}$.
6

答案： （1）$2^{5}-2^{4}=2^{4}$；$2^{n+1}-2^{n}=2^{n}$. （2）6

26. (9分)给出定义如下：我们称使等式a-b= ab+1成立的一对有理数a,b为“相伴有理数对”,记为(a,b).
例如：$3-\frac{1}{2}= 3×\frac{1}{2}+1$,$5-\frac{2}{3}= 5×\frac{2}{3}+1$,所以数对$(3,\frac{1}{2})$,$(5,\frac{2}{3})$都是“相伴有理数对”.
(1)数对$(-2,\frac{1}{3})$,$(-\frac{1}{2},-3)$中,是“相伴有理数对”的是$(-\frac{1}{2},-3)$；
(2)若(x+1,5)是“相伴有理数对”,则x的值是$-\frac{5}{2}$；
(3)若(a,b)是“相伴有理数对”,求$3ab-a+\frac{1}{2}(a+b-5ab)+1$的值.
解：$3ab - a +\frac{1}{2}(a + b - 5ab)+1=3ab - a+\frac{1}{2}a+\frac{1}{2}b-\frac{5}{2}ab + 1=\frac{1}{2}ab-\frac{1}{2}a+\frac{1}{2}b + 1=\frac{1}{2}ab-\frac{1}{2}(a - b)+1$，因为$a -b=ab + 1$，所以原式$=\frac{1}{2}ab-\frac{1}{2}(ab + 1)+1=-\frac{1}{2}+1=\frac{1}{2}$

答案： 解：（1）$(-\frac{1}{2},-3)$；（2）$-\frac{5}{2}$；（3）$3ab - a +\frac{1}{2}(a + b - 5ab)+1=3ab - a+\frac{1}{2}a+\frac{1}{2}b-\frac{5}{2}ab + 1=\frac{1}{2}ab-\frac{1}{2}a+\frac{1}{2}b + 1=\frac{1}{2}ab-\frac{1}{2}(a - b)+1$，因为$a -b=ab + 1$，所以原式$=\frac{1}{2}ab-\frac{1}{2}(ab + 1)+1=-\frac{1}{2}+1=\frac{1}{2}$