《2025年新课程自主学习与测评七年级数学上册人教版》

6. 某冷冻厂的一个冷库现在的室温是-2℃,现在一批食品需要在-30℃下冷藏,如果每小时能升温-4℃,需要几小时才能达到所需温度？

答案： $7\ h$

【阅读】在研究有理数时,一般要考虑两个方面：一是数的符号,即是正数、负数还是零；二是数的绝对值. 除了考虑符号外,有理数的运算(或大小比较)往往都归结为绝对值的运算(或大小比较),这样的“分类”或“转化”思想在数学研究中是屡见不鲜的. 下面请探索思考：
【探索】(1) 若两个数的积小于0,则这两个数的和可能为①②③(只填序号).
① 正数； ② 负数； ③ 0.
(2) 若整数a,b满足a + b = -6,则ab的最大值为9.
【拓展】(3) 若mn ≠0,直接写出$\frac{m}{|m|}\ + \frac{|n|}{n}\$的所有可能取值：-2,0,2.
(4) 若m + n＞0,试比较mn与0的大小.
$\because m+n＞0$，$\therefore m,n$中至少有一个是正数.①当$m,n$都为正数时，$mn＞0$；②当$m,n$中一个为正数，另一个为0时，$mn=0$；③当$m,n$中一个为正数，另一个为负数时，$mn＜0$.

答案： （1）①②③；
（2）9；
（3）解：根据$mn\neq 0$，①当$m>0,n>0$时，$\frac{m}{|m|}+\frac{|n|}{n}=1+1=2$；②当$m>0,n<0$时，$\frac{m}{|m|}+\frac{|n|}{n}=1-1=0$；③当$m<0,n>0$时，$\frac{m}{|m|}+\frac{|n|}{n}=-1+1=0$；④当$m<0,n<0$时，$\frac{m}{|m|}+\frac{|n|}{n}=-1-1=-2$.$\frac{m}{|m|}+\frac{|n|}{n}$的所有可能取值为$-2,0,2$.
（4）$\because m+n>0$，$\therefore m,n$中至少有一个是正数.①当$m,n$都为正数时，$mn>0$；②当$m,n$中一个为正数，另一个为0时，$mn=0$；③当$m,n$中一个为正数，另一个为负数时，$mn<0$. 

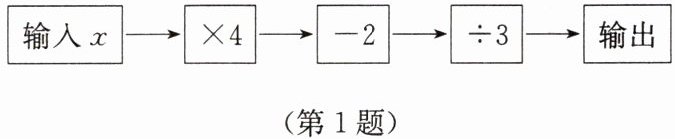
1. 如图是一个简单的数值运算程序图,当输入x的值为-1时,输出的数值为-2.
输入x → ×4 → -2 → ÷3 → 输出

答案： $-2$

2. 伍伍同学购买某种粽子,每5个花费15元,若花费45元则可购买这种粽子的个数为 (C)
A.3
B.10
C.15
D.135

答案： C

3. (-1)÷(-3)×$\frac{1}{3}$的结果是 (B)
A.-1
B.\$\frac{1}{9}\$
C.1
D.-9

答案： B

4. 下列运算有错误的是 (A)
A.\$\frac{1}{3}\$÷(-3)= 3×(-3)
B.-5÷(-\$\frac{1}{2}\$)= -5×(-2)
C.8 - (-2)= 8 + 2
D.2 - 7= (+2)+(-7)

答案： A