《2025年新课程自主学习与测评七年级数学上册人教版》

22. (6 分)下表是小明记录的 10 月份第二周内每天中午 12 时的气温的变化情况(气温比前一天上升记为正数,下降记为负数)：

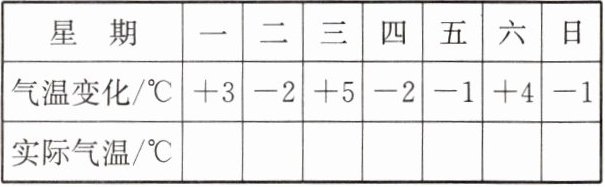
(1) 若第一周的周日中午 12 时的气温为$10^{\circ}C$,那么第二周每天的实际气温是多少？(请完成上表)
(2) 第二周的最高气温与最低气温相差多少摄氏度？

答案： （1）13,11,16,14,13,17,16；（2）$6^{\circ}C$

23. (6 分)小虫从某点$O$出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程(单位：$cm$)依次为$+5$,$-3$,$+10$,$-8$,$-6$,$+12$,$-10$.
(1) 通过计算说明小虫是否能回到起点；
(2) 如果小虫爬行的速度为$0.5cm/s$,则小虫共爬行了多少时间？

答案： （1）5-3+10-8-6+12-10=0,能回到起点；（2）(5+3+10+8+6+12+10)÷0.5=108(s)

24. (9 分)同学们都知道,$|5-(-2)|$表示 5 与$-2$之差的绝对值,实际上也可理解为 5 与$-2$两数在数轴上所对应的两点之间的距离. 试探索：
(1) $|5-(-2)|=$7；
(2) 找出所有符合条件的整数$x$,使得$|x+5|+|x-2|= 7$,这样的整数是-5,-4,-3,-2,-1,0,1,2；
(3) 由以上探索,猜想对于任何有理数$x$,$|x-3|+|x-6|$是否有最小值？如果有,写出最小值；如果没有,请说明理由.
有最小值3

答案： （1）7；（2）-5,-4,-3,-2,-1,0,1,2；（3）有最小值3

25. (12 分)观察下列两个等式：$2-\frac{1}{3}= 2× \frac{1}{3}+1$,$5-\frac{2}{3}= 5× \frac{2}{3}+1$,给出定义如下：使等式$a-b= ab+1$成立的一对有理数“$a$,$b$”为“共生有理数对”,记为$(a,b)$. 例如：数对$\left(2,\frac{1}{3}\right)$,$\left(5,\frac{2}{3}\right)$都是“共生有理数对”.
(1) 通过计算,判断数对$(1,2)$是不是“共生有理数对”；
(2) 若$(m,n)$是“共生有理数对”,则$(-n,-m)$______“共生有理数对”(填“是”或“不是”)；
(3) 如果$(m,n)$是“共生有理数对”,且$m-n= 4$,求$(-2)^{mn}$的值.
(1)∵1-2=-1,1×2+1=3,∴1-2≠1×2+1,∴数对(1,2)不是“共生理数对”.
(2)是
(3)由条件可知m-n=mn+1,∵m-n=4,∴mn+1=4,∴mn=3,∴$(-2)^{mn}=(-2)^3=-8$

答案： 解:
(1)
∵1-2=-1,1×2+1=3,
∴1-2≠1×2+1,
∴数对(1,2)不是“共生理数对”. （2）由条件可知m-n=mn+1,
∴-n-(-m)=m-n=mn+1=(-n)·(-m)+1,
∴(-n,-m)是“共生理数对”. （3）由条件可知m-n=mn+1,
∵m-n=4,
∴mn+1=4,
∴mn=3,
∴$(-2)^{mn}=(-2)^3=-8$