《2025年新课程自主学习与测评七年级数学上册人教版》

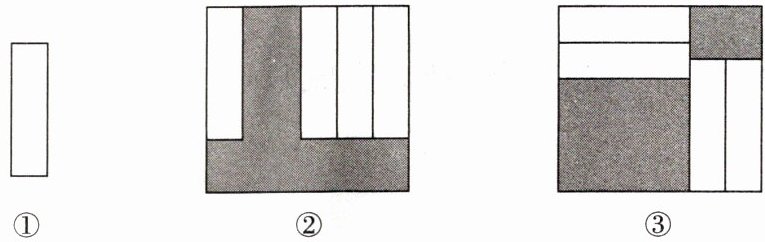
如图,把四张大小相同的长方形卡片(如图①)按图②、图③两种方式放在一个底面为长方形(长比宽多$5cm$)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为$C_{1}$,图③中阴影部分的周长为$C_{2}$,那么$C_{1}比C_{2}$大10$cm$。
]

答案： 10

1. 已知$(4x^{2} - 7x - 3) - A = 3x^{2} - 2x + 1$,则$A$为(D)
A.$x^{2} - 9x + 2$
B.$x^{2} - 9x - 4$
C.$x^{2} - 5x - 2$
D.$x^{2} - 5x - 4$

答案： D

2. 已知一个长方形的周长为$(4a + 2b)$,宽为$(a - b)$,则它的长为(A)
A.$a + 2b$
B.$a$
C.$3a + 3b$
D.$3a + b$

答案： A

3. 填空：
(1) 单项式$-3x^{2}$,$5x$,$2x^{2}$,$-2x$的和是$3x-x^2$；
(2) 比$3 - x^{2} + x少x^{3} + 5x$的多项式是$-x^3-x^2-4x+3$；
(3) 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如右图所示的一个二次三项式,则所捂的二次三项式是$x^2-2x+1$；
(4) 已知$2x - 3y = 1$,则$10 - 4x + 6y = $8。

答案： （1）$3x-x^2$；（2）$-x^3-x^2-4x+3$；（3）$x^2-2x+1$；（4）8.

4. 计算：
(1) 先化简$2(3a^{2}b - ab^{2}) - 3(-ab^{2} + 2a^{2}b)$,并求当$a = 2$,$b = -3$时的值。
(2) 已知$A = 2x^{2} - 3x - 5$,$B = -x^{2} + 2x - 3$,求$A - 2B$。

答案： （1）原式$=6a^2b-2ab^2+3ab^2-6a^2b=ab^2$,当$a=2,b=-3$时,原式$=2×(-3)^2=18$. （2）$A-2B=2x^2-3x-5-2(-x^2+2x-3)=2x^2-3x-5+2x^2-4x+6=4x^2-7x+1$.