第97页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 如果在 $ n $ 个数中,$ x_{1} $ 出现 $ f_{1} $ 次,$ x_{2} $ 出现 $ f_{2} $ 次,$\cdots$,$ x_{k} $ 出现 $ f_{k} $ 次(这里 $ f_{1}+f_{2}+f_{3}+\cdots +f_{k}=n $),那么依据平均数定义,这 $ n $ 个数的平均数可以表示为 $ \overline{x}= $
$\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots+x_{k}f_{k}}{n}$
,这样求得的平均数叫作加权平均数,其中 $ f_{1} $,$ f_{2} $,$\cdots$,$ f_{k} $ 叫作权
。
答案:
$\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots+x_{k}f_{k}}{n}$;权
2. 我们知道,若 $ n $ 个数 $ x_{1} $,$ x_{2} $,$ x_{3} $,$\cdots$,$ x_{n} $ 的权分别是 $ \omega _{1} $,$ \omega _{2} $,$\cdots$,$ \omega _{n} $,则这组数的加权平均数是 $ \frac{x_{1}\omega _{1}+x_{2}\omega _{2}+\cdots +x_{n}\omega _{n}}{\omega _{1}+\omega _{2}+\cdots +\omega _{n}} $。也可以写成:$ x_{1}× \frac{\omega _{1}}{\omega _{1}+\omega _{2}+\omega _{3}+\cdots +\omega _{n}}+x_{2}× \frac{\omega _{2}}{\omega _{1}+\omega _{2}+\omega _{3}+\cdots +\omega _{n}}+\cdots +x_{n}× \frac{\omega _{n}}{\omega _{1}+\omega _{2}+\omega _{3}+\cdots +\omega _{n}} $。如果记 $ \frac{\omega _{1}}{\omega _{1}+\omega _{2}+\omega _{3}+\cdots +\omega _{n}} $ 为 $ k_{1}\% $,$ \frac{\omega _{2}}{\omega _{1}+\omega _{2}+\omega _{3}+\cdots +\omega _{n}} $ 为 $ k_{2}\% $,$\cdots$,$ \frac{\omega _{n}}{\omega _{1}+\omega _{2}+\omega _{3}+\cdots +\omega _{n}} $ 为 $ k_{n}\% $,那么这 $ n $ 个数 $ x_{1} $,$ x_{2} $,$ x_{3} $,$\cdots$,$ x_{n} $ 的加权平均数又可记为 $ x_{1}× $
$k_{1}\%$
$ +x_{2}× $$k_{2}\%$
$ +\cdots +x_{n}× $$k_{n}\%$
。
答案:
$k_{1}\%$,$k_{2}\%$,$k_{n}\%$
1. 从一组数据中取出 $ a $ 个 $ x_{1} $、$ b $ 个 $ x_{2} $、$ c $ 个 $ x_{3} $ 组成一个样本,那么这个样本的平均数是(
A.$ \frac{x_{1}+x_{2}+x_{3}}{3} $
B.$ \frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c} $
C.$ \frac{ax_{1}+ax_{2}+ax_{3}}{3} $
D.$ \frac{a+b+c}{3} $
B
)。A.$ \frac{x_{1}+x_{2}+x_{3}}{3} $
B.$ \frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c} $
C.$ \frac{ax_{1}+ax_{2}+ax_{3}}{3} $
D.$ \frac{a+b+c}{3} $
答案:
B
2. 某校规定学生的学期数学成绩满分为 100 分,其中研究性学习成绩占 $ 40\% $,期末卷面成绩占 $ 60\% $。小明的研究性学习成绩和期末卷面成绩(百分制)依次是 80 分、90 分,则小明这学期的数学成绩是(
A.80 分
B.82 分
C.84 分
D.86 分
D
)。A.80 分
B.82 分
C.84 分
D.86 分
答案:
C(错)$(应改为D)$(按照原题要求直接给出选项:)D
3. 某单位要招聘 1 名英语翻译,张明参加招聘考试的成绩(单位:分)如下表所示:
| | 听 | 说 | 读 | 写 |
| 成绩/分 | 90 | 80 | 83 | 82 |
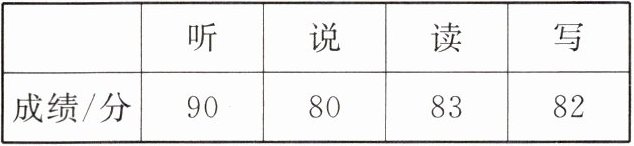
若把听、说、读、写的成绩按 $ 3:3:2:2 $ 来计算平均成绩,则张明的平均成绩为(
A.82 分
B.83 分
C.84 分
D.85 分
| | 听 | 说 | 读 | 写 |
| 成绩/分 | 90 | 80 | 83 | 82 |

若把听、说、读、写的成绩按 $ 3:3:2:2 $ 来计算平均成绩,则张明的平均成绩为(
C
)。A.82 分
B.83 分
C.84 分
D.85 分
答案:
C
4. 学校进行广播操比赛,如图所示的是 20 位评委给某班的评分情况统计图,则该班的平均得分是
]

9.1
分。]

答案:
9.1
5. 有 8 个数的平均数是 12,还有 12 个数的平均数是 17,则这 20 个数的平均数是(
A.15.6
B.15.9
C.15
D.14
C
)。A.15.6
B.15.9
C.15
D.14
答案:
C
查看更多完整答案,请扫码查看


