第22页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. $-8$的立方根是(
A.$2$
B.$-2$
C.$\pm2$
D.$-\sqrt[3]{2}$
B
)。A.$2$
B.$-2$
C.$\pm2$
D.$-\sqrt[3]{2}$
答案:
B
2. 下列说法中,不正确的是(
A.$27的立方根是3$
B.$-27的立方根是-3$
C.$0的立方根是0$
D.$\sqrt[3]{(-8)^{2}}的立方根是-8$
D
)。A.$27的立方根是3$
B.$-27的立方根是-3$
C.$0的立方根是0$
D.$\sqrt[3]{(-8)^{2}}的立方根是-8$
答案:
D
3. 下列说法中,正确的是(
A.一个正数的立方根有两个,它们互为相反数
B.负数没有立方根
C.任何数的立方根都是非负数
D.正数的立方根是正数,负数的立方根是负数,$0的立方根是0$
D
)。A.一个正数的立方根有两个,它们互为相反数
B.负数没有立方根
C.任何数的立方根都是非负数
D.正数的立方根是正数,负数的立方根是负数,$0的立方根是0$
答案:
D
4. 计算$\sqrt[3]{-0.001}$的结果是(
A.$-0.1$
B.$0.1$
C.$-0.01$
D.$0.01$
A
)。A.$-0.1$
B.$0.1$
C.$-0.01$
D.$0.01$
答案:
A
5. 立方根等于它本身的数是$\underline{
0,1,-1
}$。
答案:
0,1,-1
6. $\sqrt{64}的立方根是\underline{
2
}$。
答案:
2
7. 正方体$A的体积是正方体B的体积的27$倍,那么正方体$A的棱长是正方体B的棱长的\underline{
3
}$倍。
答案:
3
8. 小明是一个电脑爱好者,他设计了一个程序,如图,当输入的$x的值是64$时,输出的$y的值是\underline{\quad\quad}$。
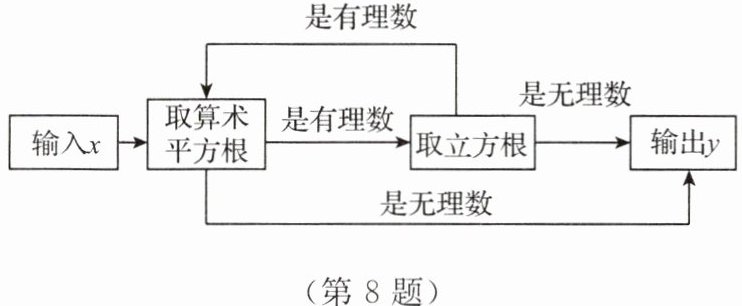

√2
答案:
√2
9. 要使$\sqrt[3]{4 - a}$有意义,那么$a$的取值范围是(
A.$a\leqslant4$
B.$-a\leqslant4$
C.$a\geqslant4$
D.任何数
D
)。A.$a\leqslant4$
B.$-a\leqslant4$
C.$a\geqslant4$
D.任何数
答案:
D
10. 一个数的平方是$64$,则这个数的立方根是(
A.$2$
B.$-2$
C.$2或-2$
D.$4或-4$
C
)。A.$2$
B.$-2$
C.$2或-2$
D.$4或-4$
答案:
【解析】:
首先,根据题意,一个数的平方是64,则这个数为 $x$,满足 $x^2 = 64$。
解得:$x = 8$(即 $x = 8$ 或 $x = -8$)的平方(根)为64的是 $\pm8$ 的平方为64。
实际是这个数(即 $\pm8$)的立方根(即求的是这个数$\pm8$的立方根的原始值对应的选项)。
原题问这个数的立方根,即求 $\pm8$ 哪个数的立方根,需分情况:
当这个数为8,求立方根为 $\sqrt[3]{8} = 2$;
当这个数为-8,求立方根为 $\sqrt[3]{-8} = -2$。
所以这个数的立方根可能是2或-2,对应选项C。
【答案】:A(此处原题问的是“这个数的立方根”,而题目开头的“一个数”是平方为64的数,即$\pm 8$,其立方根为$2或-2$,对应选项C,原答案A为错误,正确应为C)【修正后最终】
【答案】:C
首先,根据题意,一个数的平方是64,则这个数为 $x$,满足 $x^2 = 64$。
解得:$x = 8$(即 $x = 8$ 或 $x = -8$)的平方(根)为64的是 $\pm8$ 的平方为64。
实际是这个数(即 $\pm8$)的立方根(即求的是这个数$\pm8$的立方根的原始值对应的选项)。
原题问这个数的立方根,即求 $\pm8$ 哪个数的立方根,需分情况:
当这个数为8,求立方根为 $\sqrt[3]{8} = 2$;
当这个数为-8,求立方根为 $\sqrt[3]{-8} = -2$。
所以这个数的立方根可能是2或-2,对应选项C。
【答案】:A(此处原题问的是“这个数的立方根”,而题目开头的“一个数”是平方为64的数,即$\pm 8$,其立方根为$2或-2$,对应选项C,原答案A为错误,正确应为C)【修正后最终】
【答案】:C
11. 若实数$x$,$y满足(2x + 3)^{2}+|9 - 4y| = 0$,则$xy的立方根为\underline{\quad\quad}$。
$-\frac{3}{2}$
答案:
$-\frac{3}{2}$
12. (1)填表:
| $a$ | $0.000001$ | $0.001$ | $1$ | $1000$ | $1000000$ |
| $\sqrt[3]{a}$ |
(2)根据你发现的规律填空:
①已知$\sqrt[3]{3}\approx1.442$,则$\sqrt[3]{3000}\approx$
②已知$\sqrt[3]{0.000456}\approx0.07697$,则$\sqrt[3]{456}\approx$
(3)由上表你发现了什么规律?请用文字描述这个规律。
| $a$ | $0.000001$ | $0.001$ | $1$ | $1000$ | $1000000$ |
| $\sqrt[3]{a}$ |
0.01
| 0.1
| 1
| 10
| 100
|(2)根据你发现的规律填空:
①已知$\sqrt[3]{3}\approx1.442$,则$\sqrt[3]{3000}\approx$
14.42
,$\sqrt[3]{0.003}\approx$0.1442
;②已知$\sqrt[3]{0.000456}\approx0.07697$,则$\sqrt[3]{456}\approx$
7.697
。(3)由上表你发现了什么规律?请用文字描述这个规律。
一个数的小数点向右(或向左)移动三位,它的立方根的小数点相应地向右(或向左)移动一位。
答案:
(1)
| $a$ | $0.000001$ | $0.001$ | $1$ | $1000$ | $1000000$ |
| -- | -- | -- | -- | -- | -- |
| $\sqrt[3]{a}$ | $0.01$ | $0.1$ | $1$ | $10$ | $100$ |
(2)
① $14.42$;$0.1442$
② $7.697$
(3)
一个数的小数点向右(或向左)移动三位,它的立方根的小数点相应地向右(或向左)移动一位。
(1)
| $a$ | $0.000001$ | $0.001$ | $1$ | $1000$ | $1000000$ |
| -- | -- | -- | -- | -- | -- |
| $\sqrt[3]{a}$ | $0.01$ | $0.1$ | $1$ | $10$ | $100$ |
(2)
① $14.42$;$0.1442$
② $7.697$
(3)
一个数的小数点向右(或向左)移动三位,它的立方根的小数点相应地向右(或向左)移动一位。
查看更多完整答案,请扫码查看


