《2025年同步练习册北京师范大学出版社八年级数学上册北师大版》

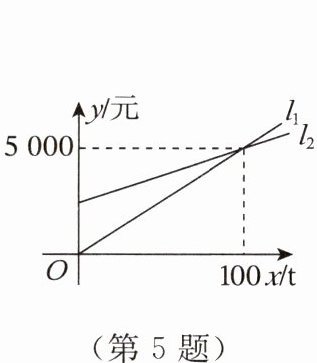
5. 如图,直线$l_1$反映了某商品的销售收入与销售量之间的关系,直线$l_2$反映了该商品的成本与销售量之间的关系,当销售收入大于成本时,该商品开始赢利,当销售量$x$＞100$t$时,该商品开始赢利。

答案： $＞100$

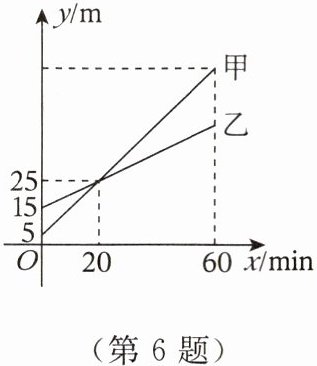
6. 甲、乙两只气球分别从不同高度同时匀速上升$60min$,气球所在位置距离地面的高度$y(m)与气球上升的时间x(min)$之间的关系如图所示。给出下列说法：①甲气球上升过程中$y与x之间的关系式为y = 2x + 5$；②$10min$时,甲气球在乙气球上方；③当两只气球高度差为$15m$时,上升时间为$50min$；④上升$60min$,乙气球距离地面高度为$40m$。其中错误的有①②④。(填序号)

答案： ①②④

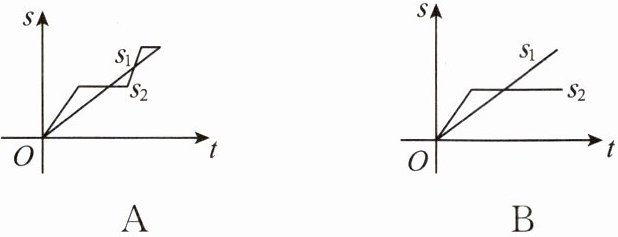
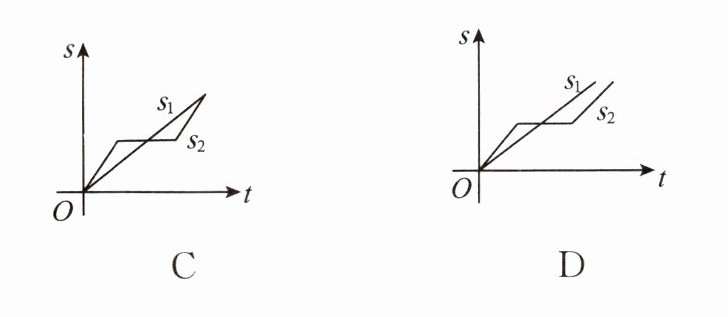
7. “龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉。当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点。用$s_1$,$s_2$分别表示乌龟和兔子所行的路程,$t$表示时间,则下列图象中与故事情节相吻合的是(B)。

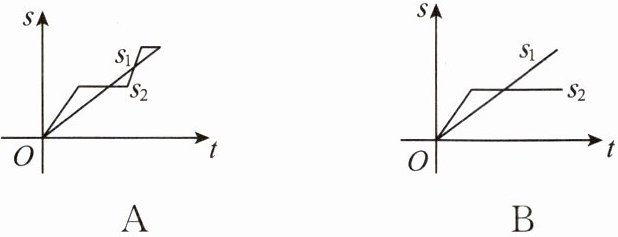
答案： 答案：B。

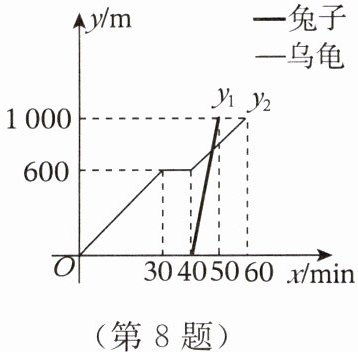
8. “龟兔赛跑”后,输了比赛的兔子没有气馁,总结反思之后,和乌龟约定再赛一场。如图所示的是“龟兔再次赛跑”时所行路程$y(m)与时间x(min)$之间的关系,$y_1$表示兔子所行路程,$y_2$表示乌龟所行路程,给出下列说法：①乌龟在途中休息了$10min$；②兔子和乌龟同时从起点出发；③兔子在乌龟出发$40\sim50min$期间追上乌龟；④乌龟和兔子再次赛跑的全程为$1000m$。其中正确的是①③④。(填序号)

答案： ①③④

9. $A$,$B两地相距300km$,甲、乙两车同时从$A地出发前往B$地,如图所示的是甲、乙两车行驶路程$y(km)随行驶时间t(h)$变化的图象,结合图象信息,回答下列问题：

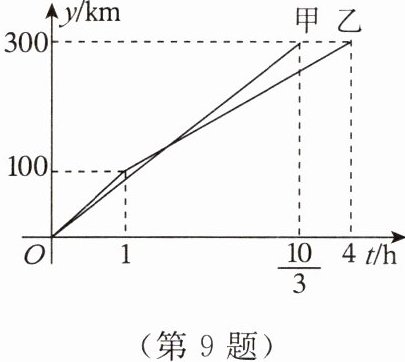
(1)甲车的速度为______$km/h$；
(2)当甲、乙两车相距$10km$时,乙车行驶的时间为______$h$。
(1)甲车的速度为90$km/h$；
(2)当甲、乙两车相距$10km$时,乙车行驶的时间为1或$\frac{29}{9}$$h$。

答案：
(1) 由图象可知，甲车行驶300km到达B地所用时间为$\frac{10}{3}h$，根据速度公式$v = \frac{s}{t}$，甲车速度为$300÷\frac{10}{3}=90km/h$。
(2) 设乙车速度为$v$，由图象可知乙车在$t = 1h$时行驶路程为100km，故乙车速度$v=100km/h$，乙车到达B地时间为$300÷100 = 3h$。
甲车路程函数：$y_{甲}=90t$；乙车路程函数：$y_{乙}=100t(t\leq3h)$，$y_{乙}=300(t＞3h)$。
情况1：乙车到达B地前（$t\leq3h$），两车相距10km，即$|100t - 90t|=10$，解得$t = 1h$。
情况2：乙车到达B地后（$t＞3h$），甲车继续行驶，两车相距10km，即$300 - 90t=10$，解得$t=\frac{29}{9}h$。
综上，乙车行驶时间为$1h$或$\frac{29}{9}h$。
(1) 90
(2) 1或$\frac{29}{9}$