第53页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 下列函数中,$y是x$的正比例函数的是(
A.$y= -2x+1$
B.$y= -\frac{1}{3}x$
C.$y= 2x^{2}$
D.$y= \frac{1}{x}$
B
)。A.$y= -2x+1$
B.$y= -\frac{1}{3}x$
C.$y= 2x^{2}$
D.$y= \frac{1}{x}$
答案:
B
2. 如图,一块长为5m、宽为2m的长方形木板,现要在长边上截去长为$x$m的一部分,则剩余木板的面积(空白部分)$y(m^{2})与x(m)$之间的关系式为(
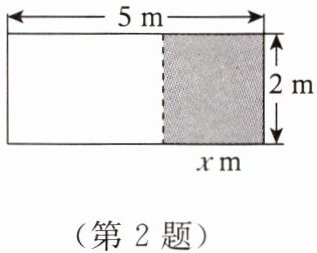
A.$y= 10-x$
B.$y= 5x$
C.$y= 2x$
D.$y= -2x+10$
D
)。
A.$y= 10-x$
B.$y= 5x$
C.$y= 2x$
D.$y= -2x+10$
答案:
D
3. 某单位需租一辆40座的客车,甲出租车公司的收费标准:服务费200元,里程费每千米10元;乙出租车公司的收费标准:每千米15元(不足1km按1km计算)。假设该单位的用车里程为60km,建议选择(
A.甲公司
B.乙公司
C.甲公司或乙公司
D.无法确定
A
)。A.甲公司
B.乙公司
C.甲公司或乙公司
D.无法确定
答案:
A
4. 某数学兴趣小组通过实验估计某液体的沸点,经过几次测量,得到以下数据:
|加热时间$t/s$|0|10|20|30|
|温度$/^{\circ}C$|15|25|35|45|
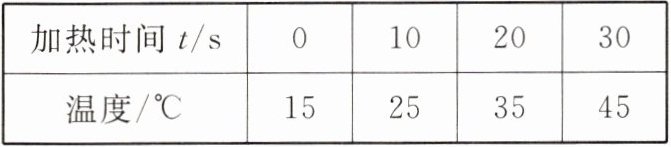
当加热80s时,该液体沸腾,则其沸点温度是(
A.$100^{\circ}C$
B.$90^{\circ}C$
C.$85^{\circ}C$
D.$95^{\circ}C$
|加热时间$t/s$|0|10|20|30|
|温度$/^{\circ}C$|15|25|35|45|

当加热80s时,该液体沸腾,则其沸点温度是(
D
)。A.$100^{\circ}C$
B.$90^{\circ}C$
C.$85^{\circ}C$
D.$95^{\circ}C$
答案:
D
5. 地球某地,温度$T(^{\circ}C)与高度d(m)之间的关系可以近似地用T= 10-\frac{d}{150}$来表示,根据这个关系,当$d$的值为900时,相应的$T$的值是
4
。
答案:
4
6. 一盘蚊香长97cm,在室内点燃后每小时燃烧16cm,则蚊香剩余的长度$y(cm)与燃烧的时间x(h)$之间的关系式为
$y=97-16x$
,当蚊香的长度小于1cm时会自动熄灭,那么这盘蚊香最多可以燃烧6
h。
答案:
$y=97-16x$;6
7. 我国是一个水资源缺乏的国家。为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水量不超过$6m^{3}$时,水价为每立方米2元,超过$6m^{3}$时,超过的部分按每立方米3元收费。该市某户居民5月用水$x m^{3}$,应交水费$y$元。
(1)若$0<x\leqslant6$,请写出$y与x$之间的关系式;
(2)若$x>6$,请写出$y与x$之间的关系式;
(3)如果某户居民这个月交水费27元,那么这个月该户居民用了多少立方米水?
(1)若$0<x\leqslant6$,请写出$y与x$之间的关系式;
(2)若$x>6$,请写出$y与x$之间的关系式;
(3)如果某户居民这个月交水费27元,那么这个月该户居民用了多少立方米水?
答案:
答题卡:
(1) 根据题意,当 $0 < x \leqslant 6$ 时,水费 $y$ 与用水量 $x$ 之间的关系是线性关系,且水价为每立方米2元。
$y = 2x$
(2) 当 $x > 6$ 时,前 $6m^{3}$ 的水费是 $2 × 6 = 12$ 元,超过的部分按每立方米3元收费。
$y = 12 + 3(x - 6)$
$y = 3x - 6$
(3) 设该户居民这个月用了 $x m^{3}$ 水,应交水费27元。
由于 $2 × 6 = 12 < 27$,所以该户居民用水量超过 $6m^{3}$,代入 $y = 3x - 6$ 得:
$3x - 6 = 27$
$3x = 33$
$x = 11$
答:这个月该户居民用了 $11m^{3}$ 水。
(1) 根据题意,当 $0 < x \leqslant 6$ 时,水费 $y$ 与用水量 $x$ 之间的关系是线性关系,且水价为每立方米2元。
$y = 2x$
(2) 当 $x > 6$ 时,前 $6m^{3}$ 的水费是 $2 × 6 = 12$ 元,超过的部分按每立方米3元收费。
$y = 12 + 3(x - 6)$
$y = 3x - 6$
(3) 设该户居民这个月用了 $x m^{3}$ 水,应交水费27元。
由于 $2 × 6 = 12 < 27$,所以该户居民用水量超过 $6m^{3}$,代入 $y = 3x - 6$ 得:
$3x - 6 = 27$
$3x = 33$
$x = 11$
答:这个月该户居民用了 $11m^{3}$ 水。
查看更多完整答案,请扫码查看


