《2025年同步练习册北京师范大学出版社八年级数学上册北师大版》

8. 如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆 $ 8\,m $ 处,发现此时绳子末端距离地面 $ 2\,m $,则旗杆的高度(滑轮上方的部分忽略不计)为17。
]

答案： 17

9. 如图,在一块四边形 $ ABCD $ 空地种植草皮,测得 $ AB = 3\,m $,$ BC = 4\,m $,$ DA = 13\,m $,$ CD = 12\,m $,且 $ \angle ABC = 90° $。若每平方米草皮需要 $ 200 $ 元,则需要投资(B)。

A.$ 16800 $ 元
B.$ 7200 $ 元
C.$ 5100 $ 元
D.无法确定
]

答案： B

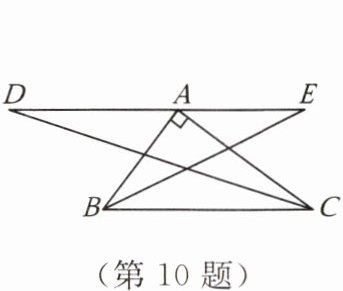
10. 如图,在 $ Rt\triangle ABC $ 中,$ \angle BAC = 90° $,过顶点 $ A $ 的直线 $ DE // BC $,$ \angle ABC $,$ \angle ACB $ 的平分线分别交 $ DE $ 于点 $ E $,$ D $。若 $ AB = 6 $,$ BC = 10 $,则 $ DE = $(B)。

A.$ 12 $
B.$ 14 $
C.$ 16 $
D.$ 18 $
]

答案： B

11. 如图,某隧道的横截面由半圆和长方形构成,其中长方形的长为 $ 5\,m $,宽为 $ 2.5\,m $,一辆卡车装满货物后,高为 $ 4.3\,m $,宽为 $ 3\,m $,它能(填“能”或“不能”)通过该隧道。
]

答案： 1. 隧道横截面由长方形和半圆组成，长方形长5m（即半圆直径），宽2.5m（长方形高度），故半圆半径$ r = \frac{5}{2} = 2.5m $。
2. 卡车宽3m，行驶时两侧距隧道中心线距离为$ \frac{3}{2} = 1.5m $。
3. 在距中心线1.5m处，半圆部分高度由勾股定理得：$ h_{半圆} = \sqrt{r^2 - 1.5^2} = \sqrt{2.5^2 - 1.5^2} = \sqrt{6.25 - 2.25} = \sqrt{4} = 2m $。
4. 此处隧道总高度为长方形高度与半圆高度之和：$ 2.5 + 2 = 4.5m $。
5. 卡车高4.3m，$ 4.5m ＞ 4.3m $，能通过。
能

12. 如图,$ \triangle ABC $ 是一张纸片,$ \angle C = 90° $,$ AC = 6 $,$ BC = 8 $,现将其折叠,使点 $ B $ 与点 $ A $ 重合,折痕为 $ DE $,则 $ DE $ 的长为$\frac{15}{4}$。
]

答案： $\frac{15}{4}$

13. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90° $,$ BC = 8 $,点 $ D $ 是 $ AC $ 边上的一个动点,将 $ \triangle ABC $ 沿 $ BD $ 所在的直线折叠,点 $ C $ 的对应点为点 $ E $,若 $ CD = 6 $,则 $ C $,$ E $ 两点之间的距离为48/5。
]

答案： 48/5

14. 【数学应用】台风是一种自然灾害,有极强的破坏力。如图,台风中心沿东西方向由 $ A $ 向 $ B $ 移动,已知 $ C $ 为一海港,且 $ AC = 300\,km $,$ BC = 400\,km $,$ AB = 500\,km $,台风中心的移动速度为 $ 25\,km/h $。经测量,距离台风中心 $ 260\,km $ 及以内的地区会受到影响。海港 $ C $ 会受到台风影响吗？若会受到台风影响,请求出受影响的时间有多长；若不会受到台风影响,请说明理由。
]

答案： 会受到影响。
1. 判断是否受影响：
由AC=300km，BC=400km，AB=500km，得AC²+BC²=300²+400²=250000=500²=AB²，故△ABC为直角三角形（∠C=90°）。
设C到AB的距离为h，由面积公式得：$\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot h$，即$300×400=500h$，解得$h=240km$。
因240km＜260km，故海港C会受台风影响。
2. 计算受影响时间：
在AB上取点D、E，使CD=CE=260km，设C到AB的垂足为F，则CF=240km。
在Rt△CFD中，$FD=\sqrt{CD²-CF²}=\sqrt{260²-240²}=\sqrt{10000}=100km$，同理FE=100km。
故DE=FD+FE=200km，受影响时间$t=\frac{DE}{速度}=\frac{200}{25}=8h$。
结论：受影响时间为8小时。