第21页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
13. 求下列各式中 $ x $ 的值:
(1) $ 4x^{2}-121 = 0 $;
(2) $ 6(x + 1)^{2}-18 = 0 $;
(3) $ (3x + 2)^{2}= 16 $;
(4) $ \frac{1}{2}(2x - 1)^{2}= 2 $。
(1) $ 4x^{2}-121 = 0 $;
(2) $ 6(x + 1)^{2}-18 = 0 $;
(3) $ (3x + 2)^{2}= 16 $;
(4) $ \frac{1}{2}(2x - 1)^{2}= 2 $。
答案:
(1)
由$4x^{2}-121 = 0$,
得$4x^{2}=121$,
$x^{2}=\frac{121}{4}$,
根据平方根定义$x=\pm\sqrt{\frac{121}{4}}$,
$x = \pm\frac{11}{2}$。
(2)
由$6(x + 1)^{2}-18 = 0$,
得$6(x + 1)^{2}=18$,
$(x + 1)^{2}=3$,
根据平方根定义$x + 1=\pm\sqrt{3}$,
$x=-1\pm\sqrt{3}$。
(3)
由$(3x + 2)^{2}=16$,
根据平方根定义$3x + 2=\pm\sqrt{16}=\pm4$,
当$3x + 2 = 4$时,$3x=2$,$x=\frac{2}{3}$;
当$3x + 2=-4$时,$3x=-6$,$x = - 2$。
所以$x=\frac{2}{3}$或$x=-2$。
(4)
由$\frac{1}{2}(2x - 1)^{2}=2$,
得$(2x - 1)^{2}=4$,
根据平方根定义$2x - 1=\pm\sqrt{4}=\pm2$,
当$2x - 1 = 2$时,$2x=3$,$x=\frac{3}{2}$;
当$2x - 1=-2$时,$2x=-1$,$x=-\frac{1}{2}$。
所以$x=\frac{3}{2}$或$x=-\frac{1}{2}$。
(1)
由$4x^{2}-121 = 0$,
得$4x^{2}=121$,
$x^{2}=\frac{121}{4}$,
根据平方根定义$x=\pm\sqrt{\frac{121}{4}}$,
$x = \pm\frac{11}{2}$。
(2)
由$6(x + 1)^{2}-18 = 0$,
得$6(x + 1)^{2}=18$,
$(x + 1)^{2}=3$,
根据平方根定义$x + 1=\pm\sqrt{3}$,
$x=-1\pm\sqrt{3}$。
(3)
由$(3x + 2)^{2}=16$,
根据平方根定义$3x + 2=\pm\sqrt{16}=\pm4$,
当$3x + 2 = 4$时,$3x=2$,$x=\frac{2}{3}$;
当$3x + 2=-4$时,$3x=-6$,$x = - 2$。
所以$x=\frac{2}{3}$或$x=-2$。
(4)
由$\frac{1}{2}(2x - 1)^{2}=2$,
得$(2x - 1)^{2}=4$,
根据平方根定义$2x - 1=\pm\sqrt{4}=\pm2$,
当$2x - 1 = 2$时,$2x=3$,$x=\frac{3}{2}$;
当$2x - 1=-2$时,$2x=-1$,$x=-\frac{1}{2}$。
所以$x=\frac{3}{2}$或$x=-\frac{1}{2}$。
14. 计算下列题目:
$ \sqrt{2^{2}}= $
$ \sqrt{2.5^{2}}= $
$ \sqrt{(-3)^{2}}= $
$ \sqrt{0^{2}}= $
$ \sqrt{(\frac{3}{5})^{2}}= $
$ \sqrt{(-\frac{2}{3})^{2}}= $
请根据计算结果,回答下列问题:
(1) $ \sqrt{a^{2}} $ 一定等于 $ a $ 吗?你发现其中的规律了吗?请用自己的语言描述出来。
(2) 利用你总结的规律,计算:
① $ \sqrt{(2-\sqrt{5})^{2}}= $
② 若 $ a>4 $,试化简 $ \sqrt{a^{2}-6a + 9}+\left|a - 4\right| $。
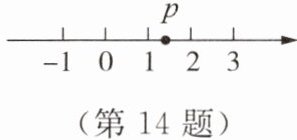
(3) 如图所示的是数 $ p $ 在数轴上的对应点的位置,化简 $ \sqrt{(p - 1)^{2}}+\sqrt{(p - 2)^{2}} $。
$ \sqrt{2^{2}}= $
2
;$ \sqrt{2.5^{2}}= $
2.5
;$ \sqrt{(-3)^{2}}= $
3
;$ \sqrt{0^{2}}= $
0
;$ \sqrt{(\frac{3}{5})^{2}}= $
$\frac{3}{5}$
;$ \sqrt{(-\frac{2}{3})^{2}}= $
$\frac{2}{3}$
。请根据计算结果,回答下列问题:
(1) $ \sqrt{a^{2}} $ 一定等于 $ a $ 吗?你发现其中的规律了吗?请用自己的语言描述出来。
不一定,规律为:$\sqrt{a^{2}} = |a|$。
(2) 利用你总结的规律,计算:
① $ \sqrt{(2-\sqrt{5})^{2}}= $
$\sqrt{5}-2$
;② 若 $ a>4 $,试化简 $ \sqrt{a^{2}-6a + 9}+\left|a - 4\right| $。
$\sqrt{a^{2}-6a + 9}+\left|a - 4\right| = |a-3| + |a-4|$,因为$a>4$,所以$|a-3| + |a-4| = a-3 + a-4 = 2a-7$。
(3) 如图所示的是数 $ p $ 在数轴上的对应点的位置,化简 $ \sqrt{(p - 1)^{2}}+\sqrt{(p - 2)^{2}} $。

由数轴可知$1 < p < 2$,$\sqrt{(p - 1)^{2}}+\sqrt{(p - 2)^{2}} = |p - 1| + |p - 2| = p - 1 + 2 - p = 1$。
答案:
$ \sqrt{2^{2}}= 2$;
$ \sqrt{2.5^{2}}= 2.5$;
$ \sqrt{(-3)^{2}}= 3$;
$ \sqrt{0^{2}}= 0$;
$ \sqrt{(\frac{3}{5})^{2}}= \frac{3}{5}$;
$ \sqrt{(-\frac{2}{3})^{2}}= \frac{2}{3}$;
(1) 不一定,规律为:$ \sqrt{a^{2}} = |a| $。
(2) ① $ \sqrt{(2-\sqrt{5})^{2}}= |2-\sqrt{5}| = \sqrt{5}-2 $;
② $ \sqrt{a^{2}-6a + 9}+\left|a - 4\right| = |a-3| + |a-4| $,
因为 $ a>4 $,
所以 $ |a-3| + |a-4| = a-3 + a-4 = 2a-7 $。
(3) 由数轴可知 $ 1 < p < 2 $,
$ \sqrt{(p - 1)^{2}}+\sqrt{(p - 2)^{2}} = |p - 1| + |p - 2| = p - 1 + 2 - p = 1 $。
$ \sqrt{2.5^{2}}= 2.5$;
$ \sqrt{(-3)^{2}}= 3$;
$ \sqrt{0^{2}}= 0$;
$ \sqrt{(\frac{3}{5})^{2}}= \frac{3}{5}$;
$ \sqrt{(-\frac{2}{3})^{2}}= \frac{2}{3}$;
(1) 不一定,规律为:$ \sqrt{a^{2}} = |a| $。
(2) ① $ \sqrt{(2-\sqrt{5})^{2}}= |2-\sqrt{5}| = \sqrt{5}-2 $;
② $ \sqrt{a^{2}-6a + 9}+\left|a - 4\right| = |a-3| + |a-4| $,
因为 $ a>4 $,
所以 $ |a-3| + |a-4| = a-3 + a-4 = 2a-7 $。
(3) 由数轴可知 $ 1 < p < 2 $,
$ \sqrt{(p - 1)^{2}}+\sqrt{(p - 2)^{2}} = |p - 1| + |p - 2| = p - 1 + 2 - p = 1 $。
查看更多完整答案,请扫码查看


