《2025年同步练习册北京师范大学出版社八年级数学上册北师大版》

1. 整数和______分数统称有理数。

答案： 整数 分数

2. 在解决实际问题的过程中,我们会发现存在这样一类数,它们既不是整数,也不是分数,即除了有理数外,还存在一类不是有理数的数。比如当$x^{2}= 6$时,$x$既不是整数,也不是分数,所以$x$一定不是有理数。

答案： 有理数；分数

1. 在等式$x^{2}= 3$中,下列说法正确的是(D)。
A.$x$是整数
B.$x$是分数
C.$x$是有理数
D.$x$不是有理数

答案： D

2. 正方形的面积为$10$,则它的边长$x$(D)。
A.是分数
B.是有限小数
C.是整数
D.不是有理数

答案： D

3. 下列正方形中,边长不是有理数的是(D)。
A.面积为$64$的正方形
B.面积为$16$的正方形
C.面积为$1.44$的正方形
D.面积为$12$的正方形

答案： D

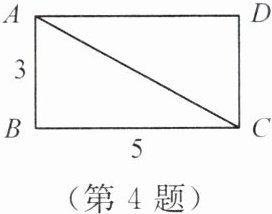
4. 如图,在长方形$ABCD$中,$AB = 3$,$BC = 5$,由勾股定理,可知$AC^{2}=$34,而$5^{2}$＜$AC^{2}$＜$6^{2}$(填“$＞$”“$＜$”或“$=$”),$AC$的长是介于整数5与6之间的一个数,而且这个数更接近整数6。

答案： $AC^2 = 34$；
$5^2 ＜ AC^2 ＜ 6^2$；
$AC$ 的长度介于整数 5 和 6 之间，更接近整数 6。
填空答案依次为：34，＜，＜，5，6，6。

5. 已知正数$m满足m^{2}= 39$,则$m$的整数部分为6。

答案： $6$

6. 如图,$B$,$C$是一个生活小区的两个路口,$BC的长为2\mathrm{km}$,$A$处是一个花园,从$A到B$,$C两路口的距离都是2\mathrm{km}$,现要从花园到生活小区修一条最短的路,这条路的长可能是整数吗？可能是分数吗？

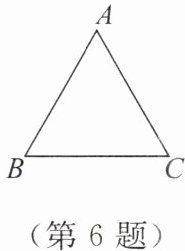
答案： 解：由题意，A到B、C距离均为2km，BC=2km，故△ABC为等边三角形。从A到生活小区最短路径为BC边上的高AD。
在等边△ABC中，BC=2km，D为BC中点，BD=1km。在Rt△ABD中，由勾股定理得：AD²+BD²=AB²，即AD²+1²=2²，AD²=3，AD=√3 km。
√3是无理数，不是整数，也不是分数。
答：这条路的长不可能是整数，不可能是分数。

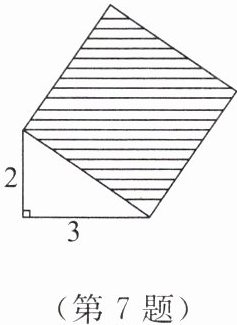
7. 如图,直角三角形两直角边的长分别是$2$,$3$,阴影部分是一个正方形,设正方形的边长为$a$。
(1)阴影部分的面积为多少？
(2)$a$是有理数吗？

答案：
(1)设直角三角形两直角边分别为3和2，正方形边长为$a$。正方形的两边分别在两直角边上，直角边上剩余线段长分别为$3 - a$和$2 - a$。由相似三角形性质得$\frac{3 - a}{3} = \frac{a}{2}$，解得$a = \frac{6}{5}$。阴影部分面积为$a^2 = \left(\frac{6}{5}\right)^2 = \frac{36}{25}$。
(2)$a = \frac{6}{5}$，是分数，属于有理数。
(1)$\frac{36}{25}$；
(2)是。