第32页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
| 相关概念 | 实数和____是一一对应的 |
| | 整数和分数 |
| | 无理数____小数 |
| | 如果一个数$x$的____等于$a$,那么这个数$x就叫作a$的平方根(或二次方根),记作____ |
| 开方 | 开平方 |
| | 引申 |
| | 二次根式 形如____的式子 |
| | 最简二次根式 被开方数____,也____ |
| | 乘除法法则 $\sqrt{a} \cdot \sqrt{b} = $____$(a \geq 0, b \geq 0)$;$\frac{\sqrt{a}}{\sqrt{b}} = $____$(a \geq 0, b > 0)$ |
| | 重要性质 $\sqrt{a^2} = $____;$\sqrt{ab} = $____$(a \geq 0, b \geq 0)$;$\sqrt{\frac{a}{b}} = $____$(a \geq 0, b > 0)$ |
| | 开立方 如果一个数$x的立方等于a$,那么这个数$x就叫作a$的____(或____),记作____ |
| 运算 | 运算法则 |
| | 运算律 加、减、乘、除、乘方、开方 |
| | 运算顺序 加法____、____;乘法____、____、____ |
| | 先算____,再算____,最后算____,有括号的要先算____ |
| | 整数和分数 |
| | 无理数____小数 |
| | 如果一个数$x$的____等于$a$,那么这个数$x就叫作a$的平方根(或二次方根),记作____ |
| 开方 | 开平方 |
| | 引申 |
| | 二次根式 形如____的式子 |
| | 最简二次根式 被开方数____,也____ |
| | 乘除法法则 $\sqrt{a} \cdot \sqrt{b} = $____$(a \geq 0, b \geq 0)$;$\frac{\sqrt{a}}{\sqrt{b}} = $____$(a \geq 0, b > 0)$ |
| | 重要性质 $\sqrt{a^2} = $____;$\sqrt{ab} = $____$(a \geq 0, b \geq 0)$;$\sqrt{\frac{a}{b}} = $____$(a \geq 0, b > 0)$ |
| | 开立方 如果一个数$x的立方等于a$,那么这个数$x就叫作a$的____(或____),记作____ |
| 运算 | 运算法则 |
| | 运算律 加、减、乘、除、乘方、开方 |
| | 运算顺序 加法____、____;乘法____、____、____ |
| | 先算____,再算____,最后算____,有括号的要先算____ |
答案:
数轴上的点;有理数;无限不循环;平方;$\pm\sqrt{a}$;$\sqrt{a}(a\geq0)$;不含分母;不含能开得尽方的因数或因式;$\sqrt{ab}$;$\sqrt{\frac{a}{b}}$;$\vert a\vert$;$\sqrt{a}\cdot\sqrt{b}$;$\frac{\sqrt{a}}{\sqrt{b}}$;立方根;三次方根;$\sqrt[3]{a}$;交换律;结合律;交换律;结合律;分配律;乘方、开方;乘除;加减;括号里面的
1. 将下列各数填在相应的集合里。
$\sqrt[3]{64}$,$\pi$,$3.1415926$,$-0.456$,$\frac{5}{11}$,$-\sqrt[3]{9}$,$3.030030003…$(相邻两个$3之间0的个数逐次加1$),$0$,$\sqrt{(-7)^2}$,$\sqrt{0.1}$。
有理数集合:…$\{
无理数集合:…$\{
正实数集合:…$\{
负实数集合:…$\{
$\sqrt[3]{64}$,$\pi$,$3.1415926$,$-0.456$,$\frac{5}{11}$,$-\sqrt[3]{9}$,$3.030030003…$(相邻两个$3之间0的个数逐次加1$),$0$,$\sqrt{(-7)^2}$,$\sqrt{0.1}$。
有理数集合:…$\{
$\sqrt[3]{64}, 3.1415926, -0.456, \frac{5}{11}, 0, \sqrt{(-7)^2}$
\}$;无理数集合:…$\{
$\pi, -\sqrt[3]{9}, 3.030030003…($相邻两个3之间0的个数逐次加$1), \sqrt{0.1}$
\}$;正实数集合:…$\{
$\sqrt[3]{64}, \pi, 3.1415926, \frac{5}{11}, 3.030030003…($相邻两个3之间0的个数逐次加$1), \sqrt{(-7)^2}, \sqrt{0.1}$
\}$;负实数集合:…$\{
$-0.456, -\sqrt[3]{9}$
\}$。
答案:
有理数集合:$\{\sqrt[3]{64}, 3.1415926, -0.456, \frac{5}{11}, 0, \sqrt{(-7)^2}\}$;
无理数集合:$\{\pi, -\sqrt[3]{9}, 3.030030003\ldots(相邻两个3之间0的个数逐次加1), \sqrt{0.1}\}$;
正实数集合:$\{\sqrt[3]{64}, \pi, 3.1415926, \frac{5}{11}, 3.030030003\ldots(相邻两个3之间0的个数逐次加1), \sqrt{(-7)^2}, \sqrt{0.1}\}$;
负实数集合:$\{-0.456, -\sqrt[3]{9}\}$。
无理数集合:$\{\pi, -\sqrt[3]{9}, 3.030030003\ldots(相邻两个3之间0的个数逐次加1), \sqrt{0.1}\}$;
正实数集合:$\{\sqrt[3]{64}, \pi, 3.1415926, \frac{5}{11}, 3.030030003\ldots(相邻两个3之间0的个数逐次加1), \sqrt{(-7)^2}, \sqrt{0.1}\}$;
负实数集合:$\{-0.456, -\sqrt[3]{9}\}$。
2. 如图,每个小正方形的边长为$1$。
(1) 图中阴影部分的面积为
(2) 估计边长$a$在相邻两个整数
(3) 设边长$a的整数部分为x$,小数部分为$y$,求$x - y$的相反数。
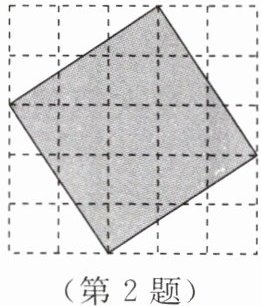
(1) 图中阴影部分的面积为
10
,阴影部分的边长$a$为√10
;(2) 估计边长$a$在相邻两个整数
3
与4
之间;(3) 设边长$a的整数部分为x$,小数部分为$y$,求$x - y$的相反数。

√10 - 6
答案:
(1) 10;√10
(2) 3;4
(3) √10 - 6
(1) 10;√10
(2) 3;4
(3) √10 - 6
查看更多完整答案,请扫码查看


