第3页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
10. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$D为AC$上一点,且$DA = DB = 5$。已知$\triangle DAB的面积为10$,则$DC$的长是
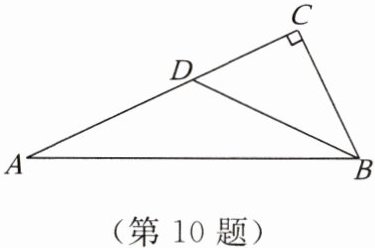
3
。
答案:
3
11. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC = 15$,$AC = 20$,$CD是AB$边上的高。求:
(1)$AB$的长;
(2)$CD$的长。
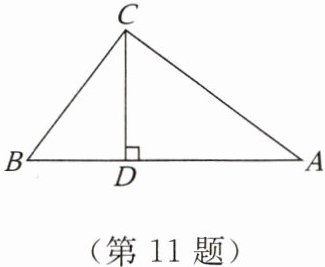
(1)$AB$的长;
(2)$CD$的长。

答案:
(1) 在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC = 15$,$AC = 20$,
根据勾股定理:
$AB = \sqrt{BC^{2} + AC^{2}} = \sqrt{15^{2} + 20^{2}} = \sqrt{225 + 400} = \sqrt{625} = 25$,
所以$AB$的长为$25$。
(2) 根据直角三角形的面积公式,有:
$S_{\triangle ABC} = \frac{1}{2} × BC × AC = \frac{1}{2} × AB × CD$,
代入已知数值,得:
$\frac{1}{2} × 15 × 20 = \frac{1}{2} × 25 × CD$,
化简得:
$15 × 20 = 25 × CD$,
$CD = \frac{15 × 20}{25} = 12$,
所以$CD$的长为$12$。
(1) 在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$BC = 15$,$AC = 20$,
根据勾股定理:
$AB = \sqrt{BC^{2} + AC^{2}} = \sqrt{15^{2} + 20^{2}} = \sqrt{225 + 400} = \sqrt{625} = 25$,
所以$AB$的长为$25$。
(2) 根据直角三角形的面积公式,有:
$S_{\triangle ABC} = \frac{1}{2} × BC × AC = \frac{1}{2} × AB × CD$,
代入已知数值,得:
$\frac{1}{2} × 15 × 20 = \frac{1}{2} × 25 × CD$,
化简得:
$15 × 20 = 25 × CD$,
$CD = \frac{15 × 20}{25} = 12$,
所以$CD$的长为$12$。
12. 【数学应用】如图,身高为$1.6\ m$的小明($AB$)想利用“勾股定理”计算出风筝的高度$CE$,已知他测得$BD的长度为25\ m$,并根据手中剩余线的长度计算出风筝线$BC的长为65\ m$。求风筝的高度$CE$。
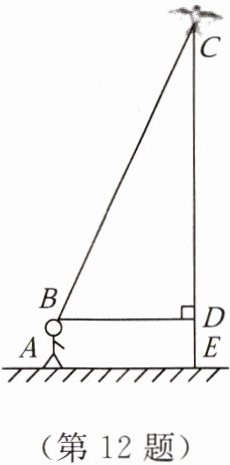

答案:
解:由题意知,四边形ABDE为矩形,
所以AB=DE=1.6m,BD=AE=25m,∠CDB=90°。
在Rt△CBD中,∠CDB=90°,BC=65m,BD=25m,
根据勾股定理得:CD²+BD²=BC²,
即CD²+25²=65²,
CD²=65²-25²=(65-25)(65+25)=40×90=3600,
所以CD=60m(负值舍去)。
因为CE=CD+DE,
所以CE=60+1.6=61.6m。
答:风筝的高度CE为61.6m。
所以AB=DE=1.6m,BD=AE=25m,∠CDB=90°。
在Rt△CBD中,∠CDB=90°,BC=65m,BD=25m,
根据勾股定理得:CD²+BD²=BC²,
即CD²+25²=65²,
CD²=65²-25²=(65-25)(65+25)=40×90=3600,
所以CD=60m(负值舍去)。
因为CE=CD+DE,
所以CE=60+1.6=61.6m。
答:风筝的高度CE为61.6m。
13. 【数学文化】2002年8月,国际数学家大会在北京举行,这是21世纪全世界数学家的一次大聚会,这次大会会标的主要图案就取材于我国古代数学家赵爽用来证明勾股定理的弦图(如图所示),这充分肯定了我国数学的成就,也弘扬了我国古代的数学文化。弦图是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形。若大正方形的面积是$13$,小正方形的面积是$1$,直角三角形中较短的直角边的长度为$a$,较长的直角边的长度为$b$,请求出$(a + b)^{2}$的值。


答案:
25
查看更多完整答案,请扫码查看


