《2025年同步练习册北京师范大学出版社八年级数学上册北师大版》

1. 若两个变量 $ x,y $ 之间的对应关系可以表示成 $ y = kx + b $($ k,b $ 为常数,$ k \neq 0 $)的形式,则称 $ y $ 是 $ x $ 的 一次函数。特别地,当 $ b = $ 0时,称 $ y $ 是 $ x $ 的 正比例函数,所以说 正比例函数 是一种特殊的一次函数。

答案： $ y = kx + b $ ，一次函数，0，正比例函数，正比例函数

2. 对一次函数而言,自变量每增加 $ 1 $,函数值就增加 k,函数值的变化是“均匀”的,因此,一次函数 $ y = kx + b $($ k,b $ 为常数,$ k \neq 0 $)中的 $ k $ 体现了一个变化过程中,函数值的变化速度。

答案： $k$

1. 下列函数是关于 $ x $ 的一次函数的是(C)。
A.$ y = \frac{1}{x} $
B.$ y = 2x^2 + 1 $
C.$ y = 3 - \frac{1}{2}x $
D.$ y = \sqrt{x} $

答案： C

2. 下列关系是正比例关系的是(D)。
A.当路程 $ s $ 一定时,速度 $ v $ 与时间 $ t $
B.圆的面积 $ S $ 与圆的半径 $ r $
C.正方体的体积 $ V $ 与棱长 $ a $
D.正方形的周长 $ C $ 与它的边长 $ a $

答案： D

3. 若函数 $ y = (m - 1)x^{m^2} + 3 $ 是一次函数,则 $ m $ 的值为(A)。
A.$ -1 $
B.$ 1 $
C.$ 0 $
D.$ \pm 1 $

答案： A

4. 若函数 $ y = (m - 2)x + (5 - m) $ 是关于 $ x $ 的一次函数,则 $ m $ 应满足的条件是$m \neq 2$；若此函数是正比例函数,则 $ m $ 的值为$5$,此时函数表达式为$y = 3x$。

答案： $m \neq 2$；$5$；$y = 3x$

5. 某辆汽车油箱中原有汽油 $ 100 \, L $,汽车每行驶 $ 1 \, km $ 耗油 $ 0.18 \, L $,那么油箱中的余油量 $ y(L) $ 与汽车行驶路程 $ x(km) $ 之间的关系式为 $y = 100 - 0.18x$,$ y $ 是(填“是”或“不是”)$ x $ 的一次函数,$ y $ 不是(填“是”或“不是”)$ x $ 的正比例函数。

答案： 关系式为 $y = 100 - 0.18x$；是；不是。

6. 小明准备买 $ a $ 本练习本,已知练习本的单价为 $ 3 $ 元。
(1) 写出小明所花的钱数 $ y $(元)与购买的本数 $ a $(本)之间的关系式；
(2) 当 $ a = 6 $ 时,求 $ y $ 的值。

答案：
(1) 因为总价=单价×数量，已知单价为3元，购买本数为$a$，所以$y = 3a$。
(2) 当$a = 6$时，$y = 3×6 = 18$。

7. 将长为 $ 30 \, cm $、宽为 $ 10 \, cm $ 的长方形白纸按如图所示的方法黏合起来,黏合部分的宽是 $ 3 \, cm $。设 $ x $ 张白纸黏合后的总长度是 $ y \, cm $。
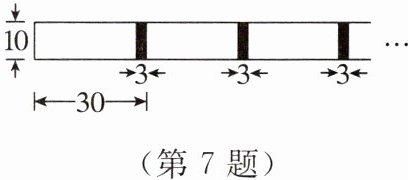
(1) 写出 $ y $ 与 $ x $ 之间的关系式,并判断 $ y $ 是不是 $ x $ 的一次函数；
(2) 当 $ x = 20 $ 时,求 $ y $ 的值。

答案：
(1) 每张纸的长度为 $30 \, cm$，每黏合一次，总长度减少 $3 \, cm$，因此 $x$ 张纸黏合后的总长度为：
$y = 30x - 3(x - 1) = 27x + 3$，
$y$ 是 $x$ 的一次函数。
(2) 当 $x = 20$ 时，
$y = 27 × 20 + 3 = 543$。