第17页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. 图①、图②均为长方形,则在图①中,$a$所满足的等式是
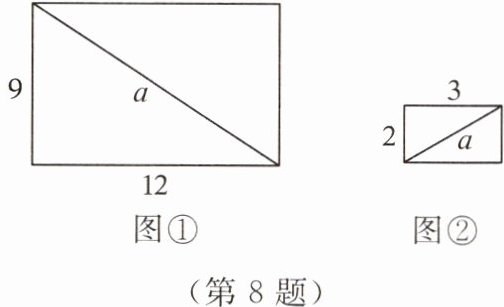
$a^2 = 9^2 + 12^2$
,$a$是一个有理数
(填“有理数”或“无理数”);在图②中,$a$所满足的等式是$a^2 = 2^2 + 3^2$
,$a$是一个无理数
(填“有理数”或“无理数”)。
答案:
$a^2 = 9^2 + 12^2$;有理数;$a^2 = 2^2 + 3^2$;无理数
9. 把下列各数写入相应的集合中:
$0$,$3$,$2.75$,$-6$,$0.8$,$\frac{\pi}{4}$,$1.212 121…$,$\frac{22}{7}$,$0.101 001 000 1…$(相邻两个$1之间0的个数逐次加1$)。
(1)有理数集合:…$\{\}$;
(2)整数集合:…$\{\}$;
(3)正数集合:…$\{\}$;
(4)分数集合:…$\{\}$。
$0$,$3$,$2.75$,$-6$,$0.8$,$\frac{\pi}{4}$,$1.212 121…$,$\frac{22}{7}$,$0.101 001 000 1…$(相邻两个$1之间0的个数逐次加1$)。
(1)有理数集合:…$\{\}$;
(2)整数集合:…$\{\}$;
(3)正数集合:…$\{\}$;
(4)分数集合:…$\{\}$。
答案:
(1)有理数集合:$\{0, 3, 2.75, -6, 0.8, 1.212121…, \frac{22}{7}\}$;
(2)整数集合:$\{0, 3, -6\}$;
(3)正数集合:$\{3, 2.75, 0.8, \frac{\pi}{4}, 1.212121…, \frac{22}{7}, 0.1010010001…\}$;
(4)分数集合:$\{2.75, 0.8, 1.212121…, \frac{22}{7}\}$。
(1)有理数集合:$\{0, 3, 2.75, -6, 0.8, 1.212121…, \frac{22}{7}\}$;
(2)整数集合:$\{0, 3, -6\}$;
(3)正数集合:$\{3, 2.75, 0.8, \frac{\pi}{4}, 1.212121…, \frac{22}{7}, 0.1010010001…\}$;
(4)分数集合:$\{2.75, 0.8, 1.212121…, \frac{22}{7}\}$。
10. 某地为发展渔业,要挖一个长方体形的鱼塘。已知鱼塘的长是宽的$2$倍,面积是$1 600 m^{2}$,则鱼塘的宽大约是多少米?(结果精确到$1 m$)
答案:
设鱼塘的宽为$x$米,则长为$2x$米。
根据长方形面积公式,有:
$x × 2x = 1600$,
$2x^{2} = 1600$,
$x^{2} = 800$,
由于$x$为宽度,取正值,所以:
$x = \sqrt{800} \approx 28$,
答:鱼塘的宽大约是$28$米。
根据长方形面积公式,有:
$x × 2x = 1600$,
$2x^{2} = 1600$,
$x^{2} = 800$,
由于$x$为宽度,取正值,所以:
$x = \sqrt{800} \approx 28$,
答:鱼塘的宽大约是$28$米。
11. 【数学文化】公元前$5$世纪,古希腊毕达哥拉斯学派的一个成员希帕索斯发现,一些数不能用整数之比来表示,如边长为$1$的正方形的对角线的长就无法用整数或整数之比来表示。这个发现动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌。据说,希帕索斯为此被投入了大海。
毕达哥拉斯学派的发现,第一次向人们揭示了有理数的缺陷,证明它不能同连续的无限直线同等看待,有理数并没有布满数轴上的点,在数轴上存在着不能用有理数表示的“孔隙”,这种“孔隙”经后人证明简直多得“不可胜数”。$15$世纪意大利著名画家达·芬奇称之为“无理的数”,$17$世纪德国天文学家开普勒称之为“不可名状”的数。然而,真理毕竟是湮没不了的,毕达哥拉斯学派抹杀真理才是“无理”。人们为了纪念希帕索斯这位为真理而献身的可敬学者,就把不可通约的量取名为“无理数”——这便是“无理数”的由来。
同学们,你们能发现身边的无理数吗?
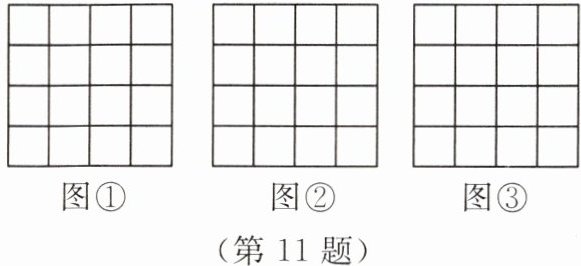
如图,在下面的正方形网格中,每个小正方形的边长都是$1$,每个小格的顶点都叫作格点,以格点为顶点,分别按下列要求画图。
(1)在图①中,画出一个三角形,使它的三边长都是有理数;
(2)在图②中,画出一个直角三角形,使它的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积为$10$。
毕达哥拉斯学派的发现,第一次向人们揭示了有理数的缺陷,证明它不能同连续的无限直线同等看待,有理数并没有布满数轴上的点,在数轴上存在着不能用有理数表示的“孔隙”,这种“孔隙”经后人证明简直多得“不可胜数”。$15$世纪意大利著名画家达·芬奇称之为“无理的数”,$17$世纪德国天文学家开普勒称之为“不可名状”的数。然而,真理毕竟是湮没不了的,毕达哥拉斯学派抹杀真理才是“无理”。人们为了纪念希帕索斯这位为真理而献身的可敬学者,就把不可通约的量取名为“无理数”——这便是“无理数”的由来。
同学们,你们能发现身边的无理数吗?
如图,在下面的正方形网格中,每个小正方形的边长都是$1$,每个小格的顶点都叫作格点,以格点为顶点,分别按下列要求画图。
(1)在图①中,画出一个三角形,使它的三边长都是有理数;
(2)在图②中,画出一个直角三角形,使它的三边长都是无理数;
(3)在图③中,画一个正方形,使它的面积为$10$。

答案:
(1)连接格点(0,0),(3,0),(0,4),得到三边长分别为3,4,5的三角形(答案不唯一)。
(2)连接格点(0,0),(1,2),(3,1),得到直角三角形,三边长分别为√5,√5,√10(答案不唯一)。
(3)连接格点(1,0),(4,1),(3,4),(0,3),得到面积为10的正方形(答案不唯一)。
(2)连接格点(0,0),(1,2),(3,1),得到直角三角形,三边长分别为√5,√5,√10(答案不唯一)。
(3)连接格点(1,0),(4,1),(3,4),(0,3),得到面积为10的正方形(答案不唯一)。
查看更多完整答案,请扫码查看


