《2025年同步练习册北京师范大学出版社八年级数学上册北师大版》

4. 如图,已知点 $ M $, $ N $ 是线段 $ AB $ 上的两点, $ AM = MN = 2 $, $ NB = 1 $,以点 $ A $ 为圆心,以 $ AN $ 的长为半径画弧；再以点 $ B $ 为圆心,以 $ BM $ 的长为半径画弧,两弧交于点 $ C $,连接 $ AC $, $ BC $,则 $ \triangle ABC $ 一定是(B)。

A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
]

答案： B

5. 如图所示的一块菜地, $ AD = 12 \ m $, $ CD = 9 \ m $, $ \angle ADC = 90° $, $ AB = 39 \ m $, $ BC = 36 \ m $,这块菜地的面积为$216m^{2}$。
]

答案： $216m^{2}$

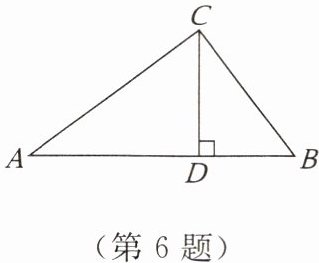
6. 如图,已知在 $ \triangle ABC $ 中, $ CD \perp AB $ 于点 $ D $, $ AC = 20 $, $ BC = 15 $, $ BD = 9 $。
(1) 求 $ CD $, $ AB $ 的长；
(2) 试说明 $ \triangle ABC $ 是直角三角形。
]

答案：
(1)在$Rt\triangle CDB$中，$CD\perp AB$，$BC=15$，$BD=9$，由勾股定理得：$CD^{2}=BC^{2}-BD^{2}=15^{2}-9^{2}=225-81=144$，$\therefore CD=12$。
在$Rt\triangle ACD$中，$AC=20$，$CD=12$，由勾股定理得：$AD^{2}=AC^{2}-CD^{2}=20^{2}-12^{2}=400-144=256$，$\therefore AD=16$。
$\therefore AB=AD+BD=16+9=25$。
(2)$\because AC=20$，$BC=15$，$AB=25$，$\therefore AC^{2}+BC^{2}=20^{2}+15^{2}=400+225=625$，$AB^{2}=25^{2}=625$，$\therefore AC^{2}+BC^{2}=AB^{2}$，由勾股定理逆定理得$\triangle ABC$是直角三角形。

7. 如图,在动物园里有两只猴子在一棵树 $ CD $ 上的点 $ B $ 处, $ BC = 5 \ m $,它们都要到池塘 $ A $ 处吃东西。其中一只猴子甲先沿树爬至树底 $ C $ 处,再沿 $ CA $ 走到离树 $ 24 \ m $ 处的池塘 $ A $ 处。另一只猴子乙先爬到树顶 $ D $ 处,再沿缆绳 $ DA $ 滑到 $ A $ 处。已知猴子甲经过的路程比猴子乙经过的路程多 $ 2 \ m $,设 $ BD = x \ m $。
(1) 请用含 $ x $ 的整式表示线段 $ AD $ 的长为______ $ m $；
(2) 这棵树高多少米？
]

(1) 请用含 $ x $ 的整式表示线段 $ AD $ 的长为$27 - x$$ m $；
(2) 这棵树高多少米？
这棵树高7米。

答案：
(1) 猴子甲的路程为 $ BC + CA = 5 + 24 = 29 \, m $。猴子乙的路程为 $ BD + AD $，设 $ BD = x \, m $，由题意甲的路程比乙多 $ 2 \, m $，则乙的路程为 $ 29 - 2 = 27 \, m $，故 $ x + AD = 27 $，因此 $ AD = 27 - x $。
(2) 树高 $ CD = BC + BD = 5 + x \, m $。在 $ Rt\triangle ACD $ 中，$ AC = 24 \, m $，由勾股定理得 $ AD^2 = AC^2 + CD^2 $。将 $ AD = 27 - x $，$ CD = 5 + x $ 代入得：
$ (27 - x)^2 = 24^2 + (5 + x)^2 $
展开得 $ 729 - 54x + x^2 = 576 + x^2 + 10x + 25 $
化简得 $ 729 - 54x = 601 + 10x $
解得 $ 64x = 128 $，$ x = 2 $。
树高 $ CD = 5 + x = 5 + 2 = 7 \, m $。
(1) $ 27 - x $
(2) $ 7 \, m $

8. 如图,在 $ Rt\triangle ABC $ 中, $ \angle ACB = 90° $, $ AB = 5 \ cm $, $ AC = 3 \ cm $,动点 $ P $ 从点 $ B $ 出发沿射线 $ BC $ 以 $ 1 \ cm/s $ 的速度移动,设运动的时间为 $ t \ s $。
(1) 求 $ BC $ 边的长；
(2) 当 $ \triangle ABP $ 为直角三角形时,求 $ t $ 的值。
]

答案：
(1)在Rt△ABC中，∠ACB=90°，AB=5cm，AC=3cm，由勾股定理得BC²=AB²-AC²=5²-3²=16，
∴BC=4cm。
(2)由题意，BP=t cm，P在射线BC上。
情况1：∠APB=90°。此时AP²+BP²=AB²，AP²=AC²+PC²，PC=|BC-BP|=|4-t|。则3²+(4-t)²+t²=5²，化简得2t²-8t=0，解得t=0(舍)或t=4。
情况2：∠BAP=90°。此时AB²+AP²=BP²，AP²=AC²+PC²，PC=t-4(t＞4)。则5²+[3²+(t-4)²]=t²，化简得-8t+50=0，解得t=25/4。
综上，t=4或t=25/4。