第50页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. 如图,某人驱车在离 $A$ 地 $10\mathrm{km}$ 的 $P$ 地出发,向 $B$ 地匀速行驶,$30\mathrm{min}$ 后离 $P$ 地 $50\mathrm{km}$,设出发 $x\mathrm{h}$ 后,汽车离 $A$ 地 $y\mathrm{km}$(未到达 $B$ 地前),则 $y$ 与 $x$ 之间的关系式为(
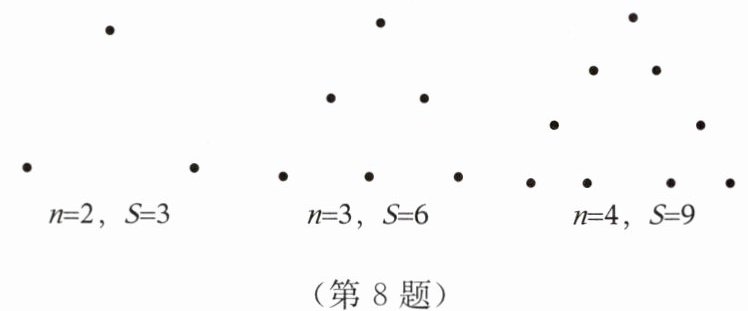
A.$S = 3n$
B.$S = 3(n - 1)$
C.$S = 3n - 1$
D.$S = 3n + 1$
B
)。
A.$S = 3n$
B.$S = 3(n - 1)$
C.$S = 3n - 1$
D.$S = 3n + 1$
答案:
B
9. 如图,某人驱车在离 $A$ 地 $10\mathrm{km}$ 的 $P$ 地出发,向 $B$ 地匀速行驶,$30\mathrm{min}$ 后离 $P$ 地 $50\mathrm{km}$,设出发 $x\mathrm{h}$ 后,汽车离 $A$ 地 $y\mathrm{km}$(未到达 $B$ 地前),则 $y$ 与 $x$ 之间的关系式为(

A.$y = 50x$
B.$y = 100x$
C.$y = 50x - 10$
D.$y = 100x + 10$
D
)。
A.$y = 50x$
B.$y = 100x$
C.$y = 50x - 10$
D.$y = 100x + 10$
答案:
D
10. 一支蜡烛长 $20\mathrm{cm}$,每分钟燃烧的长度是 $2\mathrm{cm}$,蜡烛剩余长度 $y(\mathrm{cm})$ 与燃烧时间 $x(\mathrm{min})$ 之间的关系式为
y=20-2x(0≤x≤10)
。
答案:
y=20-2x(0≤x≤10)
11. 周长为 $10\mathrm{cm}$ 的等腰三角形,腰长 $y(\mathrm{cm})$ 与底边长 $x(\mathrm{cm})$ 之间的关系式为
y=5-0.5x
,自变量的取值范围是0<x<5
。
答案:
y=5-0.5x;0<x<5
12. 如图,正方形 $ABCD$ 的边长为 $4$,点 $P$ 是正方形边上的一个动点,以 $C$ 为起点,沿 $C - B - A$ 的路径移动,设点 $P$ 经过的路径长为 $x$,$\triangle APD$ 的面积为 $y$,则 $y$ 与 $x$ 之间的关系式为
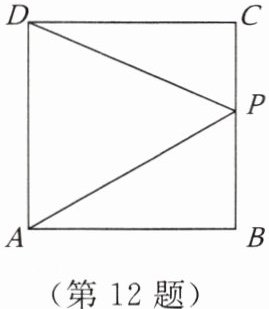
y=8(0≤x≤4),y=16-2x(4≤x≤8)
。
答案:
y=8(0≤x≤4),y=16-2x(4≤x≤8)
13. 【数学应用】某商店出售一种瓜子,其售价 $y(\mathrm{元})$ 与瓜子的质量 $x(\mathrm{kg})$ 之间的关系如下表:
|瓜子的质量 $x/\mathrm{kg}$|1|2|3|4|…|
|售价 $y/\mathrm{元}$| $20 + 0.2$ | $40 + 0.2$ | $60 + 0.2$ | $80 + 0.2$ |…|
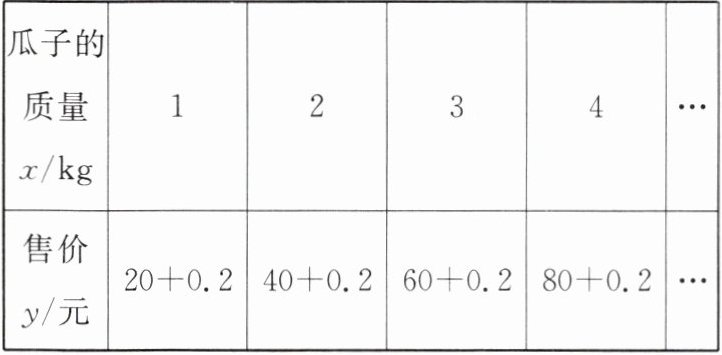
其中,售价中的 $0.2$ 元是包装的费用。
(1) 在这个变化过程中,自变量与因变量各是什么?
(2) 写出出售 $7\mathrm{kg}$ 瓜子的售价。
(3) 写出 $y$ 与 $x$ 之间的关系式。
(4) 商店规定,当一次性购买 $100\mathrm{kg}$ 及以上瓜子时,全部所购瓜子打九折。八(1)班、八(2)班正好要举办一次“党庆活动”,两个班一共 $94$ 人,每人购买 $1\mathrm{kg}$,包装费用全免。要买够两个班的瓜子,最少要花多少钱?
|瓜子的质量 $x/\mathrm{kg}$|1|2|3|4|…|
|售价 $y/\mathrm{元}$| $20 + 0.2$ | $40 + 0.2$ | $60 + 0.2$ | $80 + 0.2$ |…|

其中,售价中的 $0.2$ 元是包装的费用。
(1) 在这个变化过程中,自变量与因变量各是什么?
(2) 写出出售 $7\mathrm{kg}$ 瓜子的售价。
(3) 写出 $y$ 与 $x$ 之间的关系式。
(4) 商店规定,当一次性购买 $100\mathrm{kg}$ 及以上瓜子时,全部所购瓜子打九折。八(1)班、八(2)班正好要举办一次“党庆活动”,两个班一共 $94$ 人,每人购买 $1\mathrm{kg}$,包装费用全免。要买够两个班的瓜子,最少要花多少钱?
答案:
(1) 自变量是瓜子的质量$x$,因变量是售价$y$。
(2) 当$x=7$时,$y=20×7 + 0.2=140.2$元。
(3) $y=20x + 0.2$。
(4) 两个班共需$94\mathrm{kg}$。
情况一:购买$94\mathrm{kg}$,费用为$20×94=1880$元(包装费免)。
情况二:购买$100\mathrm{kg}$,打九折,费用为$20×0.9×100=1800$元。
$1800<1880$,最少花费$1800$元。
(1) 自变量是瓜子的质量$x$,因变量是售价$y$。
(2) 当$x=7$时,$y=20×7 + 0.2=140.2$元。
(3) $y=20x + 0.2$。
(4) 两个班共需$94\mathrm{kg}$。
情况一:购买$94\mathrm{kg}$,费用为$20×94=1880$元(包装费免)。
情况二:购买$100\mathrm{kg}$,打九折,费用为$20×0.9×100=1800$元。
$1800<1880$,最少花费$1800$元。
查看更多完整答案,请扫码查看


