第52页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. 如图,三角形是有规律地从里到外逐层排列的,设 $ y $ 为第 $ n $ 层($ n $ 为正整数)三角形的个数,则下列关系式中正确的是(
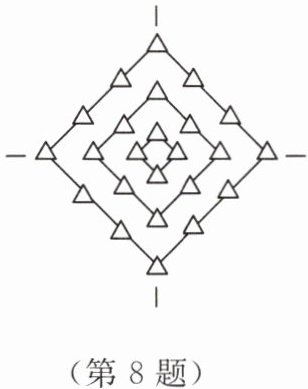
A.$ y = 4n - 4 $
B.$ y = 4n $
C.$ y = 4n + 4 $
D.$ y = n^2 $
B
)。
A.$ y = 4n - 4 $
B.$ y = 4n $
C.$ y = 4n + 4 $
D.$ y = n^2 $
答案:
B
9. 若函数 $ y = (m - 2)x^{|m| - 1} $ 是一次函数,则 $ m = $
$-2$
。
答案:
$-2$
10. 一个长方形的周长为 $ 24 $,设它的一条边长为 $ x $,那么它的面积 $ y $ 与 $ x $ 之间的关系式为
$ y = -x^2 + 12x $
,这个函数不是
(填“是”或“不是”)一次函数。
答案:
$ y = -x^2 + 12x $,不是
11. 已知函数 $ y = (m - 3)x^{3 - |m|} + m + 2 $,当 $ m = $
-2
时,$ y $ 是 $ x $ 的正比例函数;当 $ m = $ 2 或 -2
时,$ y $ 是 $ x $ 的一次函数。
答案:
-2;2 或 -2
12. 【数学应用】一旅游团来到某旅游景点,看到售票处旁边的公告栏如下图所示,请根据公告栏的内容,回答下列问题:
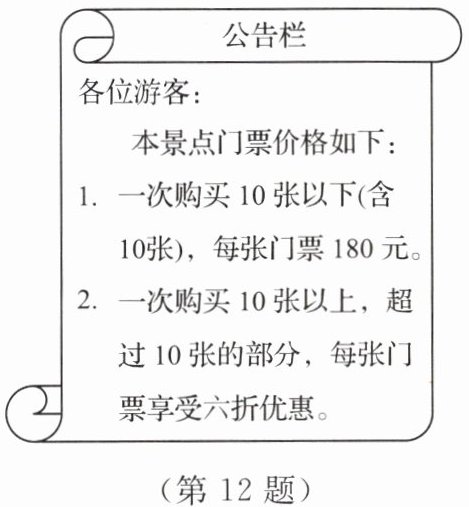
(1) 若该旅游团人数为 $ 9 $,门票费用是多少?若该旅游团人数为 $ 30 $,门票费用又是多少?
(2) 设该旅游团人数为 $ x $,写出该旅游团门票费用 $ y $(元)与人数 $ x $ 之间的关系式(直接填写在下面的横线上)。
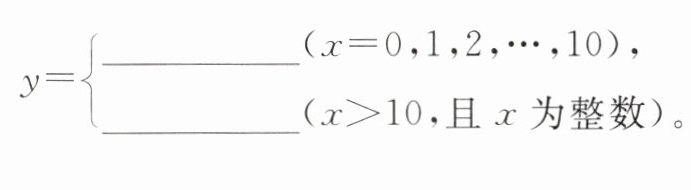
(1)
(2)

(1) 若该旅游团人数为 $ 9 $,门票费用是多少?若该旅游团人数为 $ 30 $,门票费用又是多少?
(2) 设该旅游团人数为 $ x $,写出该旅游团门票费用 $ y $(元)与人数 $ x $ 之间的关系式(直接填写在下面的横线上)。
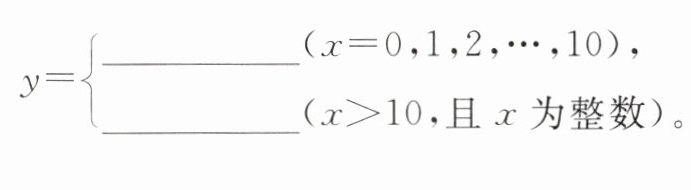
(1)
当旅游团人数为 9 时,因为 9 ≤ 10,每张门票 180 元,所以门票费用为 9 × 180 = 1620 元。当旅游团人数为 30 时,前 10 张门票费用为 10 × 180 = 1800 元,超过 10 张的部分有 30 - 10 = 20 张,这 20 张每张享受六折优惠,即每张 180 × 0.6 = 108 元,这部分费用为 20 × 108 = 2160 元,所以总门票费用为 1800 + 2160 = 3960 元。
(2)
$y = \begin{cases} 180x (x = 0,1,2,\cdots,10) \\ 108x + 720 (x > 10,且 x 为整数) \end{cases}$
答案:
(1) 当旅游团人数为 $9$ 时,因为 $9 \leq 10$,每张门票 $180$ 元,所以门票费用为 $9 × 180 = 1620$ 元。
当旅游团人数为 $30$ 时,前 $10$ 张门票费用为 $10 × 180 = 1800$ 元,超过 $10$ 张的部分有 $30 - 10 = 20$ 张,这 $20$ 张每张享受六折优惠,即每张 $180 × 0.6 = 108$ 元,这部分费用为 $20 × 108 = 2160$ 元,所以总门票费用为 $1800 + 2160 = 3960$ 元。
(2) $y = \begin{cases} 180x (x = 0,1,2,\cdots,10) \\ 108x + 720 (x > 10,且 x 为整数) \end{cases}$
(1) 当旅游团人数为 $9$ 时,因为 $9 \leq 10$,每张门票 $180$ 元,所以门票费用为 $9 × 180 = 1620$ 元。
当旅游团人数为 $30$ 时,前 $10$ 张门票费用为 $10 × 180 = 1800$ 元,超过 $10$ 张的部分有 $30 - 10 = 20$ 张,这 $20$ 张每张享受六折优惠,即每张 $180 × 0.6 = 108$ 元,这部分费用为 $20 × 108 = 2160$ 元,所以总门票费用为 $1800 + 2160 = 3960$ 元。
(2) $y = \begin{cases} 180x (x = 0,1,2,\cdots,10) \\ 108x + 720 (x > 10,且 x 为整数) \end{cases}$
13. 【数学应用】星期天,张老师提着篮子(篮子的质量为 $ 0.5 \, kg $)去集市买 $ 10 \, kg $ 鸡蛋,当张老师往篮子里拾称好的鸡蛋时,发现比过去买 $ 10 \, kg $ 鸡蛋的数量少了很多,于是她将鸡蛋装进篮子再让摊主一起称,共称得 $ 10.55 \, kg $,她立刻要求摊主退 $ 1 \, kg $ 鸡蛋的钱,她是怎样知道摊主少称了鸡蛋呢?请将分析过程写出来。由此你得到什么启示?(请用一至两句话,简要叙述出来)
答案:
设摊主称出的重量为$ M $,实际重量与称出重量的比例系数为$ x $($ x < 1 $,因秤不准导致实际重量偏小)。
1. 鸡蛋实际重量:摊主称出鸡蛋$ 10\ kg $,则鸡蛋实际重量为$ 10x\ kg $。
2. 总实际重量:篮子实际重量$ 0.5\ kg $,故鸡蛋与篮子总实际重量为$ 10x + 0.5\ kg $。
3. 联合称重关系:一起称时摊主称出$ 10.55\ kg $,其实际重量为$ 10.55x\ kg $。因此:
$ 10x + 0.5 = 10.55x $
解得$ 0.55x = 0.5 $,$ x = \frac{0.5}{0.55} = \frac{10}{11} $。
4. 鸡蛋实际重量计算:鸡蛋实际重量为$ 10x = 10 × \frac{10}{11} = \frac{100}{11} \approx 9.09\ kg $。
5. 少称重量:$ 10 - \frac{100}{11} = \frac{10}{11} \approx 1\ kg $。
启示:利用已知重量的物体可检验秤的准确性。
1. 鸡蛋实际重量:摊主称出鸡蛋$ 10\ kg $,则鸡蛋实际重量为$ 10x\ kg $。
2. 总实际重量:篮子实际重量$ 0.5\ kg $,故鸡蛋与篮子总实际重量为$ 10x + 0.5\ kg $。
3. 联合称重关系:一起称时摊主称出$ 10.55\ kg $,其实际重量为$ 10.55x\ kg $。因此:
$ 10x + 0.5 = 10.55x $
解得$ 0.55x = 0.5 $,$ x = \frac{0.5}{0.55} = \frac{10}{11} $。
4. 鸡蛋实际重量计算:鸡蛋实际重量为$ 10x = 10 × \frac{10}{11} = \frac{100}{11} \approx 9.09\ kg $。
5. 少称重量:$ 10 - \frac{100}{11} = \frac{10}{11} \approx 1\ kg $。
启示:利用已知重量的物体可检验秤的准确性。
查看更多完整答案,请扫码查看


