第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. 一个正方形的面积是$15$,估计它的边长大小在(
A.$2和3$之间
B.$3和4$之间
C.$4和5$之间
D.$5和6$之间
B
)。A.$2和3$之间
B.$3和4$之间
C.$4和5$之间
D.$5和6$之间
答案:
B
9. 如图,网格中小正方形的边长都是$1$,四边形$ABCD$的四个顶点都在格点上,四条边中长度是有理数的有(
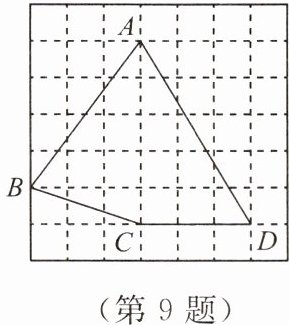
A.$1$条
B.$2$条
C.$3$条
D.$4$条
B
)。
A.$1$条
B.$2$条
C.$3$条
D.$4$条
答案:
B
10. 大家知道,当$x^{2}= 2(x>0)$时,$x$的值不可能是有理数,而$1^{2}<x^{2}<2^{2}$,所以$x的整数部分是1$。根据以上内容,解答下面的问题:
(1)若$x^{2}= 10$,则$x的整数部分m= $
(2)若$y^{2}= 17$,则$y的整数部分n= $
(3)若$m$,$n$分别是一个三角形的两条边的长,第三条边的长是$5$,则这个三角形是
(1)若$x^{2}= 10$,则$x的整数部分m= $
3
;(2)若$y^{2}= 17$,则$y的整数部分n= $
4
;(3)若$m$,$n$分别是一个三角形的两条边的长,第三条边的长是$5$,则这个三角形是
直角
三角形。
答案:
(1)
因为$3^{2}=9\lt10$,$4^{2}=16\gt10$,当$x^{2}=10(x\gt0)$时,所以$x$的整数部分$m = 3$。
(2)
因为$4^{2}=16\lt17$,$5^{2}=25\gt17$,当$y^{2}=17(y\gt0)$时,所以$y$的整数部分$n = 4$。
(3)
已知$m = 3$,$n = 4$,第三条边长是$5$。
因为$3^{2}+4^{2}=9 + 16=25=5^{2}$,满足勾股定理,所以这个三角形是直角三角形。
故答案依次为:
(1)$3$;
(2)$4$;
(3)直角。
(1)
因为$3^{2}=9\lt10$,$4^{2}=16\gt10$,当$x^{2}=10(x\gt0)$时,所以$x$的整数部分$m = 3$。
(2)
因为$4^{2}=16\lt17$,$5^{2}=25\gt17$,当$y^{2}=17(y\gt0)$时,所以$y$的整数部分$n = 4$。
(3)
已知$m = 3$,$n = 4$,第三条边长是$5$。
因为$3^{2}+4^{2}=9 + 16=25=5^{2}$,满足勾股定理,所以这个三角形是直角三角形。
故答案依次为:
(1)$3$;
(2)$4$;
(3)直角。
11. 若一个边长为$a的正方形的面积为30$,则$a$的取值范围正确的是(
A.$5.0 < a < 5.2$
B.$5.2 < a < 5.5$
C.$5.5 < a < 5.7$
D.$5.7 < a < 6.0$
B
)。A.$5.0 < a < 5.2$
B.$5.2 < a < 5.5$
C.$5.5 < a < 5.7$
D.$5.7 < a < 6.0$
答案:
B
12. 已知直角三角形的两条直角边的长度分别是$9\mathrm{cm}和5\mathrm{cm}$,斜边长是$x\mathrm{cm}$。
(1)估计$x$在哪两个整数之间。
(2)如果把$x$的结果精确到十分位,估计$x$的值;如果精确到百分位呢?用计算器验证你的估计值。
(1)估计$x$在哪两个整数之间。
(2)如果把$x$的结果精确到十分位,估计$x$的值;如果精确到百分位呢?用计算器验证你的估计值。
答案:
(1)由勾股定理得$x^2=9^2 + 5^2=81 + 25=106$。因为$10^2=100$,$11^2=121$,$100<106<121$,所以$10<x<11$,即$x$在10和11之间。
(2)因为$10.2^2=104.04$,$10.3^2=106.09$,$104.04<106<106.09$,所以$10.2<x<10.3$。又因为$10.29^2=105.8841$,$10.30^2=106.09$,$105.8841<106<106.09$,所以$10.29<x<10.30$。精确到十分位,$x\approx10.3$;精确到百分位,$x\approx10.30$。用计算器计算$\sqrt{106}\approx10.2956$,验证得精确到十分位是10.3,精确到百分位是10.30。
(1)10和11之间
(2)精确到十分位:10.3;精确到百分位:10.30
(1)由勾股定理得$x^2=9^2 + 5^2=81 + 25=106$。因为$10^2=100$,$11^2=121$,$100<106<121$,所以$10<x<11$,即$x$在10和11之间。
(2)因为$10.2^2=104.04$,$10.3^2=106.09$,$104.04<106<106.09$,所以$10.2<x<10.3$。又因为$10.29^2=105.8841$,$10.30^2=106.09$,$105.8841<106<106.09$,所以$10.29<x<10.30$。精确到十分位,$x\approx10.3$;精确到百分位,$x\approx10.30$。用计算器计算$\sqrt{106}\approx10.2956$,验证得精确到十分位是10.3,精确到百分位是10.30。
(1)10和11之间
(2)精确到十分位:10.3;精确到百分位:10.30
13.【数学应用】在以前的学习中,我们已经知道,整数和分数统称有理数。整数看作分母为$1的分数或者是小数点后是0$的小数,分数都可以化为有限小数或者无限循环小数的形式。反过来,任何有限小数和无限循环小数也都可以写成分数形式。因此,有理数都能化成分数。比如:
(1)$5可以看作\frac{5}{1}$。
(2)$2.4= \frac{24}{10}= \frac{12}{5}$。
(3)要把$0.\dot{3}$转化成分数形式,可以采用下面的方法:
设$x = 0.\dot{3}= 0.3333…$①,
则$10x = 3.3333…$②,
由②$-$①,得$9x = 3$,解得$x= \frac{1}{3}$。
因此$0.\dot{3}= 0.3333…= \frac{1}{3}$。
通过阅读以上材料,请你解答下列问题:
(1)
(2)把$0.\dot{7}$化成分数。
设$x = 0.\dot{7}=0.777\cdots$①,
则$10x = 7.777\cdots$②,
由②$-$①,得$9x = 7$,
解得$x=\frac{7}{9}$。
因此$0.\dot{7}=0.777\cdots=\frac{7}{9}$。
(1)$5可以看作\frac{5}{1}$。
(2)$2.4= \frac{24}{10}= \frac{12}{5}$。
(3)要把$0.\dot{3}$转化成分数形式,可以采用下面的方法:
设$x = 0.\dot{3}= 0.3333…$①,
则$10x = 3.3333…$②,
由②$-$①,得$9x = 3$,解得$x= \frac{1}{3}$。
因此$0.\dot{3}= 0.3333…= \frac{1}{3}$。
通过阅读以上材料,请你解答下列问题:
(1)
整数
和分数
统称有理数。有理数的表现形式有整数、有限小数、无限循环小数
,它们都能化成分数
的形式。(2)把$0.\dot{7}$化成分数。
设$x = 0.\dot{7}=0.777\cdots$①,
则$10x = 7.777\cdots$②,
由②$-$①,得$9x = 7$,
解得$x=\frac{7}{9}$。
因此$0.\dot{7}=0.777\cdots=\frac{7}{9}$。
答案:
(1)整数;分数;整数、有限小数、无限循环小数;分数。
(2)设$x = 0.\dot{7}=0.777\cdots$①,
则$10x = 7.777\cdots$②,
由②$-$①,得$9x = 7$,
解得$x=\frac{7}{9}$。
因此$0.\dot{7}=0.777\cdots=\frac{7}{9}$。
(1)整数;分数;整数、有限小数、无限循环小数;分数。
(2)设$x = 0.\dot{7}=0.777\cdots$①,
则$10x = 7.777\cdots$②,
由②$-$①,得$9x = 7$,
解得$x=\frac{7}{9}$。
因此$0.\dot{7}=0.777\cdots=\frac{7}{9}$。
查看更多完整答案,请扫码查看


