第100页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
8. 在新年晚会的投飞镖游戏环节中,5名同学的投掷成绩(单位:环)分别是7,8,7,10,8,则这组数据的离差平方和是
6
,方差为1.2
。
答案:
6,1.2
9. 小明用$s^{2}= \frac{1}{10}[(x_{1}-3)^{2}+(x_{2}-3)^{2}+…+(x_{10}-3)^{2}]$计算一组数据的方差,那么$x_{1}+x_{2}+x_{3}+…+x_{10}= $
30
。
答案:
30
10. 已知样本数据$x_{1},x_{2},…,x_{n}$的平均数是5,方差是4,则数据$2x_{1}+3$,$2x_{2}+3$,…,$2x_{n}+3$的平均数为
13
,方差为16
。
答案:
设原样本数据的平均数为$\overline{x}=5$,方差为$s^2 =4$,数据变换形式为$y_i=2x_i+3$,
对于平均数:新数据的平均数为$\overline{y}=\frac{1}{n}\sum_{i=1}^{n}(2x_i+3)=2\overline{x}+3$,
代入$\overline{x}=5$,得$\overline{y}=2×5+3=13$,
对于方差:新数据的方差为$s_y^2=\frac{1}{n}\sum_{i=1}^{n}(y_i-\overline{y})^2$,
由于$y_i-\overline{y}=2x_i+3-(2\overline{x}+3)=2(x_i-\overline{x})$,
所以$s_y^2=\frac{1}{n}\sum_{i=1}^{n}[2(x_i-\overline{x})]^2=4s^2$,
代入$s^2=4$,得$s_y^2=4×4=16$,
所以,新数据的平均数为 13,方差为 16。
对于平均数:新数据的平均数为$\overline{y}=\frac{1}{n}\sum_{i=1}^{n}(2x_i+3)=2\overline{x}+3$,
代入$\overline{x}=5$,得$\overline{y}=2×5+3=13$,
对于方差:新数据的方差为$s_y^2=\frac{1}{n}\sum_{i=1}^{n}(y_i-\overline{y})^2$,
由于$y_i-\overline{y}=2x_i+3-(2\overline{x}+3)=2(x_i-\overline{x})$,
所以$s_y^2=\frac{1}{n}\sum_{i=1}^{n}[2(x_i-\overline{x})]^2=4s^2$,
代入$s^2=4$,得$s_y^2=4×4=16$,
所以,新数据的平均数为 13,方差为 16。
11. 如图所示的是某市连续5天的天气情况。日期5月25日5月26日5月27日5月28日5月29日天气现象大雨中雨晴晴多云最高气温23${\hspace{0pt}}^{\circ }C$25${\hspace{0pt}}^{\circ }C$23${\hspace{0pt}}^{\circ }C$25${\hspace{0pt}}^{\circ }C$24${\hspace{0pt}}^{\circ }C$最低气温21${\hspace{0pt}}^{\circ }C$22${\hspace{0pt}}^{\circ }C$15${\hspace{0pt}}^{\circ }C$15${\hspace{0pt}}^{\circ }C$17${\hspace{0pt}}^{\circ }C$空气质量良优优优良
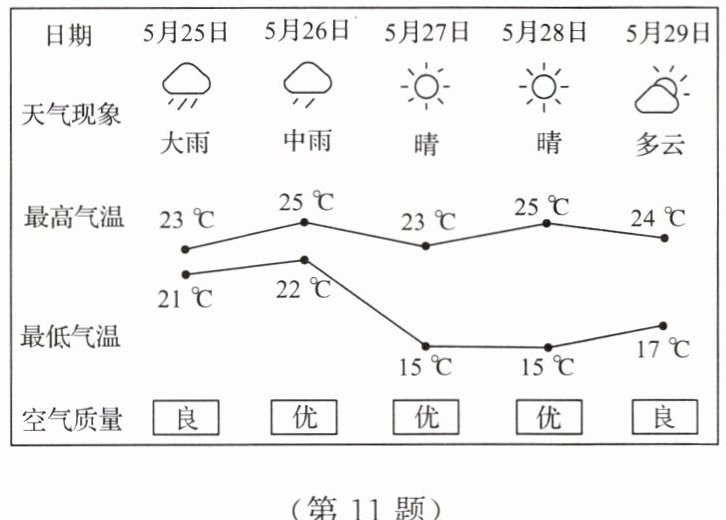
(1)利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大;
(2)根据图中提供的信息,请再写出两个不同类型的结论。

(1)利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大;
(2)根据图中提供的信息,请再写出两个不同类型的结论。
答案:
(1)
最高气温数据:23,25,23,25,24
最高气温平均数:$\overline{x}_高=\frac{23+25+23+25+24}{5}=24(^{\circ}C)$
最高气温方差:$S_高^2=\frac{(23-24)^2+(25-24)^2+(23-24)^2+(25-24)^2+(24-24)^2}{5}=\frac{1+1+1+1+0}{5}=0.8$
最低气温数据:21,22,15,15,17
最低气温平均数:$\overline{x}_低=\frac{21+22+15+15+17}{5}=18(^{\circ}C)$
最低气温方差:$S_低^2=\frac{(21-18)^2+(22-18)^2+(15-18)^2+(15-18)^2+(17-18)^2}{5}=\frac{9+16+9+9+1}{5}=8.8$
因为$8.8>0.8$,所以日最低气温波动大。
(2)
①这5天中空气质量为优的有3天,良的有2天;
②雨天(25日、26日)的最低气温(21℃、22℃)高于晴天(27日、28日)的最低气温(15℃、15℃)。
(1)
最高气温数据:23,25,23,25,24
最高气温平均数:$\overline{x}_高=\frac{23+25+23+25+24}{5}=24(^{\circ}C)$
最高气温方差:$S_高^2=\frac{(23-24)^2+(25-24)^2+(23-24)^2+(25-24)^2+(24-24)^2}{5}=\frac{1+1+1+1+0}{5}=0.8$
最低气温数据:21,22,15,15,17
最低气温平均数:$\overline{x}_低=\frac{21+22+15+15+17}{5}=18(^{\circ}C)$
最低气温方差:$S_低^2=\frac{(21-18)^2+(22-18)^2+(15-18)^2+(15-18)^2+(17-18)^2}{5}=\frac{9+16+9+9+1}{5}=8.8$
因为$8.8>0.8$,所以日最低气温波动大。
(2)
①这5天中空气质量为优的有3天,良的有2天;
②雨天(25日、26日)的最低气温(21℃、22℃)高于晴天(27日、28日)的最低气温(15℃、15℃)。
12. 某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,成绩达到60分及以上为合格,达到90分及以上为优秀。这次竞赛中,甲、乙两组学生成绩如下:
甲组:30,60,60,60,60,60,70,90,90,100;
乙组:50,60,60,60,70,70,70,70,80,90。
(1)根据以上成绩得到的统计分析表中$a=$
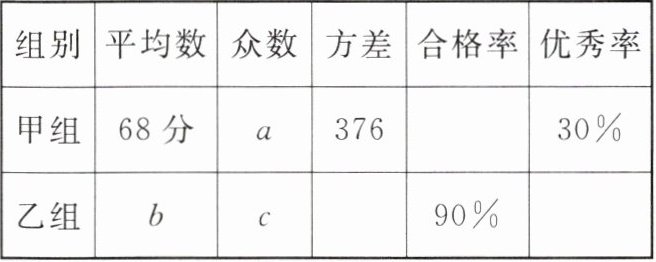
(2)计算乙组学生成绩的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?请说明理由。
乙组方差:
$\begin{aligned}\bar{x}_乙&=68\\s^2_乙&=\frac{1}{10}[(50-68)^2+3×(60-68)^2+4×(70-68)^2+(80-68)^2+(90-68)^2]\\&=\frac{1}{10}[324+3×64+4×4+144+484]\\&=\frac{1}{10}×1160=116\end{aligned}$
乙组优秀率:$\frac{1}{10}×100\%=10\%$
选择乙组,理由:乙组方差较小,成绩更稳定。
甲组:30,60,60,60,60,60,70,90,90,100;
乙组:50,60,60,60,70,70,70,70,80,90。
(1)根据以上成绩得到的统计分析表中$a=$
60
分,$b=$68
分,$c=$70
分。组别平均数众数方差合格率优秀率甲组68分$a$37630%乙组$b$$c$90%
(2)计算乙组学生成绩的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?请说明理由。
乙组方差:
$\begin{aligned}\bar{x}_乙&=68\\s^2_乙&=\frac{1}{10}[(50-68)^2+3×(60-68)^2+4×(70-68)^2+(80-68)^2+(90-68)^2]\\&=\frac{1}{10}[324+3×64+4×4+144+484]\\&=\frac{1}{10}×1160=116\end{aligned}$
乙组优秀率:$\frac{1}{10}×100\%=10\%$
选择乙组,理由:乙组方差较小,成绩更稳定。
答案:
(1)60;68;70
(2)乙组方差:
$\begin{aligned}\bar{x}_乙&=68\\s^2_乙&=\frac{1}{10}[(50-68)^2+3×(60-68)^2+4×(70-68)^2+(80-68)^2+(90-68)^2]\\&=\frac{1}{10}[324+3×64+4×4+144+484]\\&=\frac{1}{10}×1160=116\end{aligned}$
乙组优秀率:$\frac{1}{10}×100\%=10\%$
选择乙组,理由:乙组方差较小,成绩更稳定。
(1)60;68;70
(2)乙组方差:
$\begin{aligned}\bar{x}_乙&=68\\s^2_乙&=\frac{1}{10}[(50-68)^2+3×(60-68)^2+4×(70-68)^2+(80-68)^2+(90-68)^2]\\&=\frac{1}{10}[324+3×64+4×4+144+484]\\&=\frac{1}{10}×1160=116\end{aligned}$
乙组优秀率:$\frac{1}{10}×100\%=10\%$
选择乙组,理由:乙组方差较小,成绩更稳定。
查看更多完整答案,请扫码查看


