《2025年同步练习册北京师范大学出版社八年级数学上册北师大版》

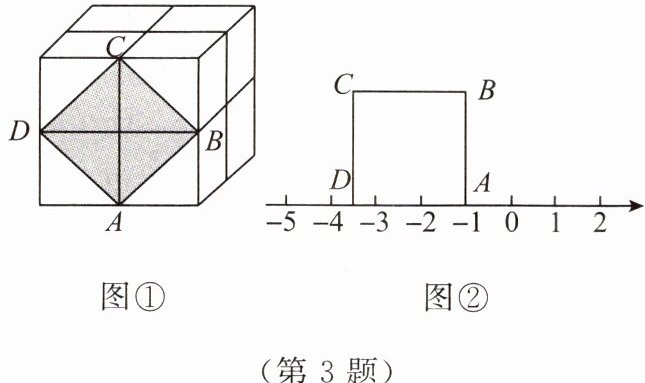
3. 如图①,这是由$8$个同样大小的小正方体组成的魔方,体积为$64$。
(1) 求出这个魔方的棱长；
(2) 图①中阴影部分是一个正方形$ABCD$,求出阴影部分的面积及其边长；
(3) 把正方形$ABCD$放到数轴上,如图②,使得点$A与-1$对应的点重合,那么点$D$在数轴上表示的数为____。

(1) 4；(2) 面积8，边长$2\sqrt{2}$；(3) -5。

答案：
(1) 设魔方棱长为$a$，由正方体体积公式$a^3 = 64$，得$a = \sqrt[3]{64} = 4$。
(2) 魔方棱长4，由8个小正方体组成，每个小正方体棱长$4÷2=2$。阴影正方形$ABCD$所在大正方体面的面积为$4×4=16$，该面被分成4个直角边为2的等腰直角三角形，每个三角形面积$\frac{1}{2}×2×2=2$，4个三角形面积和$4×2=8$，故阴影正方形面积$16 - 8 = 8$，边长$\sqrt{8}=2\sqrt{2}$。
(3) 正方形边长$2\sqrt{2}$，对角线长$2\sqrt{2}×\sqrt{2}=4$。点$A$对应$-1$，点$D$在$A$左侧，距离为对角线长4，故点$D$表示的数为$-1 - 4 = -5$。
(1) 4；
(2) 面积8，边长$2\sqrt{2}$；
(3) -5。

4. 计算：
(1) $\sqrt{8} - 3\sqrt{\frac{1}{2}} + |1 - \sqrt{2}|$；
(2) $\frac{\sqrt{4} × 2\sqrt{3}}{\sqrt{3}} - \frac{\sqrt{16}}{8} + (\pi - 3.14)^0$。

答案：
(1)
首先，化简各项：
$\sqrt{8}=\sqrt{4×2}=2\sqrt{2}$；
$3\sqrt{\frac{1}{2}} = 3×\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{2}$；
$\vert1 - \sqrt{2}\vert=\sqrt{2}-1$（因为$\sqrt{2}\approx1.414\gt1$）。
然后，代入原式计算：
$\sqrt{8}-3\sqrt{\frac{1}{2}}+\vert1 - \sqrt{2}\vert=2\sqrt{2}-\frac{3\sqrt{2}}{2}+\sqrt{2}-1$
$=(2\sqrt{2}-\frac{3\sqrt{2}}{2}+\sqrt{2})-1=\frac{4\sqrt{2}-3\sqrt{2}+2\sqrt{2}}{2}-1=\frac{3\sqrt{2}}{2}-1$。
(2)
首先，计算各项：
$\frac{\sqrt{4}×2\sqrt{3}}{\sqrt{3}}=\frac{2×2\sqrt{3}}{\sqrt{3}} = 4$；
$\frac{\sqrt{16}}{8}=\frac{4}{8}=\frac{1}{2}$；
$(\pi - 3.14)^0=1$（任何非零数的$0$次方都等于$1$）。
然后，代入原式计算：
$\frac{\sqrt{4}×2\sqrt{3}}{\sqrt{3}}-\frac{\sqrt{16}}{8}+(\pi - 3.14)^0=4-\frac{1}{2}+1=\frac{8 - 1+2}{2}=\frac{9}{2}$。
综上，
(1)的答案是$\frac{3\sqrt{2}}{2}-1$；
(2)的答案是$\frac{9}{2}$。

5. 化简求值：
$(x + y)(x - y) + y(x + 2y) - (x - y)^2$,其中$x = 2 + \sqrt{3}$,$y = 2 - \sqrt{3}$。

答案： 3

6. 【综合与实践】在学习了“勾股定理”和“实数”后,某同学以“已知三角形三边的长度,求三角形的面积”为主题开展了数学活动。
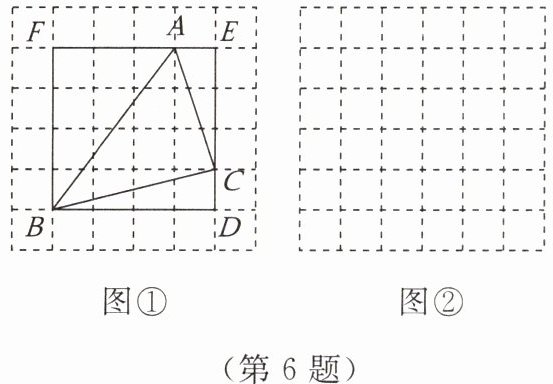
操作发现：如图,在$6 × 6$的正方形网格中,每个小正方形的边长均为$1$,在图①中画出$\triangle ABC$,同时构造正方形$BDEF$,且它的边$DE$,$EF分别经过点C$,$A$,借助此图便可求出$\triangle ABC$的面积。
实践探究：(1) 在图①所画的$\triangle ABC$中,$AB = $5,$AC = $$\sqrt{10}$,$BC = $$\sqrt{5}$,$S_{\triangle ABC} = $3.5。
(2) 在图②中的正方形网格中画出$\triangle XYZ$,使$XY = \sqrt{5}$,$XZ = \sqrt{13}$,$YZ = \sqrt{20}$,并求出$\triangle XYZ$的面积。

(2)图②中$\triangle XYZ$的顶点坐标可以选择：$X(0,0)$，$Y(2,1)$，$Z(0,4)$。$S_{\triangle XYZ} = 4$。

答案：
(1)
$AB = 5$，
$AC = \sqrt{10} $，
$BC = \sqrt{5} $，
$S_{\triangle ABC} = 3.5$。
(2)
图②中$\triangle XYZ$的顶点坐标可以选择：
$X(0,0)$，$Y(2,1)$，$Z(0,4)$。
$S_{\triangle XYZ} = 4$。