第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 据史书记载,最早的风筝是由古代匠人墨子用木头制成的木鸟,称为“木鸢”. 后来随着造纸术的发明,人们开始用纸张和竹条制作风筝,使其更加轻便、易于放飞. 在如图所示的“风筝”图案中,$AB = AD$,$∠B = ∠D$,$BC = DE$,则可以直接判定(
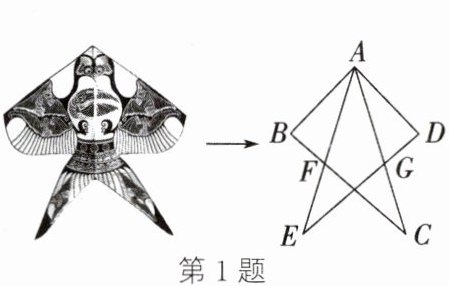
A.$△AEG≌△ABC$
B.$△AEG≌△ACF$
C.$△ABF≌△ADC$
D.$△ABC≌△ADE$
D
)
A.$△AEG≌△ABC$
B.$△AEG≌△ACF$
C.$△ABF≌△ADC$
D.$△ABC≌△ADE$
答案:
1. D
2. 数学课上,老师布置了“测量锥形瓶底面的内径”的探究任务,善思小组想到了以下方案:如图,用螺丝钉将两根长度相等的小棒$AD$,$BC$的中点$O$固定,只要测得$C$,$D$两点之间的距离,就可知道内径$AB$的长度,此方案依据的数学定理或基本事实是
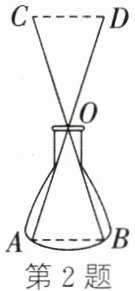
SAS
.
答案:
2. SAS
3. 如图,$AD = CB$,若可以运用“SAS”来判定$△ABC≌△CDA$,则需要添加的一个条件是
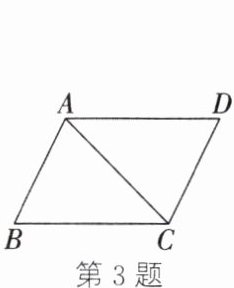
答案不唯一,如∠ACB=∠CAD
.
答案:
3. 答案不唯一,如∠ACB=∠CAD
4. 如图,$D$,$E$分别是$AB$,$AC$上的点,且$AB = AC$,$AD = AE$. 求证:$△ABE≌△ACD$.
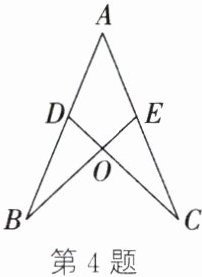

答案:
4. 在△ABE和△ACD中,$\begin{cases}AB = AC,\\\angle BAE = \angle CAD,\\AE = AD.\end{cases}$
∴△ABE≌△ACD(SAS)
∴△ABE≌△ACD(SAS)
5. 如图,$BE = CF$,$AB = DE$,若要判定$△ABC≌△DEF$,则可添加的条件是(
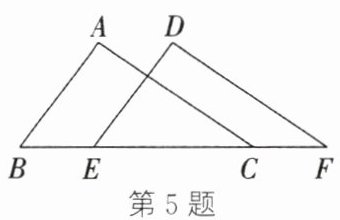
A.$BC = EF$
B.$∠A = ∠D$
C.$AC// DF$
D.$AB// DE$
D
)
A.$BC = EF$
B.$∠A = ∠D$
C.$AC// DF$
D.$AB// DE$
答案:
5. D
6. 如图,$AB$平分$∠CAD$,$E$为$AB$上一点,若$AC = AD$,则下列结论错误的是(
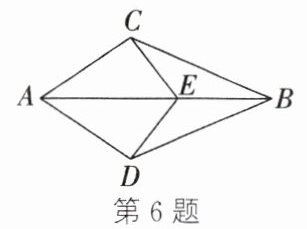
A.$BC = BD$
B.$CE = DE$
C.$BA$平分$∠CBD$
D.图中一共有两对全等三角形
D
)
A.$BC = BD$
B.$CE = DE$
C.$BA$平分$∠CBD$
D.图中一共有两对全等三角形
答案:
6. D
7. 如图,在$△ABC$中,$AD = AE$,$BD = CE$,$∠ADB = ∠AEC$,则$△$
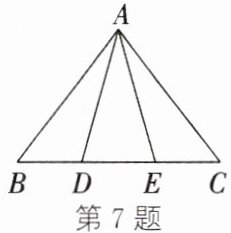
ADB
$≌△$AEC
,$△$ABE
$≌△$ACD
.
答案:
7. ADB AEC ABE ACD
8. 如图,在$△ABE$和$△DCF$中,$∠B = ∠C$,$AB = DC$,若要证明$△ABE≌△DCF$,则还需要添加一个条件:
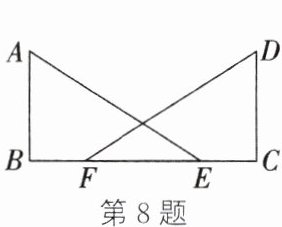
答案不唯一,如BE=CF
.(写出一种即可)
答案:
8. 答案不唯一,如BE=CF
查看更多完整答案,请扫码查看


